今回は直感的に理解しやすいように、交流の波に対する等速円運動の参考円を考えてみます。
直列回路であるので、電流 $I$ は各素子に対して共通です。
回路全体にかかる電圧 $V$ は、コイル・コンデンサー・抵抗 にかかる電圧の位相差を考えて、それらをベクトル的に合成して得ます。
電源電圧 $V$ の、数学的計算による導出は次回です。
電磁気の記事は次を参照してください。
RLC直列回路（ベクトル） 交流の基礎5
RLC直列回路
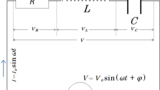
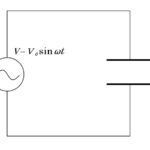
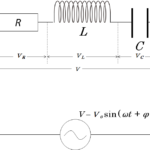
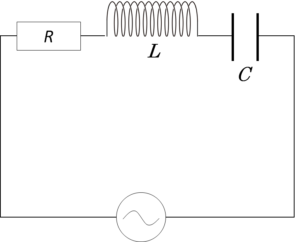いままでの交流の基礎の学習をもとに、コイル・コンデンサー・抵抗を直列に接続した図のような回路を考えます。
$V_0=ZI_0$ $V_e=ZI_e$
$Z=\sqrt{R^2 + \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }$
$I=I_0\sin \omega t$ $V=V_0 \sin (\omega t + \phi)$
RLC直列回路を流れる電流と回路全体にかかる電圧の位相差 $\phi$ は、
$\tan \phi = \dfrac{\:\omega L \:- \dfrac{1}{\omega C}\:}{R}$
コイル・コンデンサー・抵抗にかかる電圧
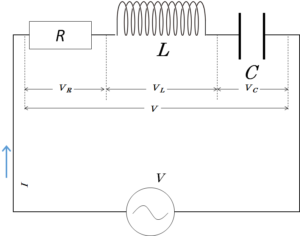
電流は直列回路のため各素子に共通です。
しかし、回路全体にかかる電圧 $V$ は各素子にかかる電圧の和ですから、抵抗にかかる電圧 $V_R$ ・ コイルにかかる電圧 $V_L$ ・ コンデンサーにかかる電圧 $V_C$ とすると、
$V=V_L+V_C+V_R$
となるはずです。
ここで各素子の最大値と実効値をそれぞれ、
- 回路全体･･････最大値 $V_0$ 実効値 $V_e$
- 抵抗･･････････最大値 $V_{R0}$ 実効値 $V_{Re}$
- コイル････････最大値 $V_{L0}$ 実効値 $V_{Le}$
- コンデンサー･･最大値 $V_{C0}$ 実効値 $V_{Ce}$
とすると、各素子にかかる電圧には位相差があるため、
最大値や実効値で単純に、
$V_0=V_{L0}+V_{C0}+V_{R0}$
$V_e=V_{Le}+V_{Ce}+V_{Re}$
とはならないことに注意します。
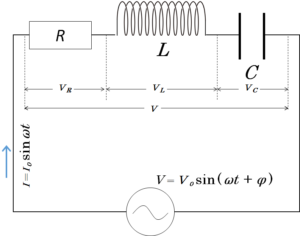
回路は直列ですから各素子を流れる電流は共通しており、今回は $I=I_0\sin \omega t$ とおくことにします（$I_0$ : 最大値）。
いま、電流の位相を先に考えたので、回路全体にかかる電圧の位相はまだわかりません。
おそらく電流に対していくらかの位相のずれを生じているはずですから、
$V=V_0\sin(\omega t + \phi)$
のような形 ($\phi$ は位相差) になると考えられます。
$\phi$ は普通、 $\dfrac{\pi}{2}$ とは違う値をとります。
位相差
各素子にかかる電圧を考えます。このとき、各素子に共通の電流を $I=I_0\sin \omega t$ としたことと、電流と電圧に関しての位相のずれから、各素子の電圧は次のように書けます。
- 抵抗 $R$ にかかる電圧 $V_R$ は、電流 $I=I_0\sin \omega t$ と同位相ですから
$V_R=V_{R0} \sin \omega t$ - コイル $L$ にかかる電圧 $V_L$ は、電流 $I=I_0\sin \omega t$ に対して $\dfrac{\pi}{2}$ 進んでいるため
$V_L=V_{L0} \sin (\omega t + \dfrac{\pi}{2})$ - コンデンサー $C$ にかかる電圧 $V_C$ は、電流 $I=I_0\sin \omega t$ に対して $\dfrac{\pi}{2}$ 遅れているため
$V_C=V_{C0} \sin (\omega t \: – \dfrac{\pi}{2})$
電圧のグラフ
ここで各素子の電圧を縦軸に、時間を横軸にとったグラフを描いて見ます。
各素子の時間 $t$ に対する電圧の値はそれぞれ、
-
- $V_R=V_{R0} \sin \omega t$
- $V_L=V_{L0} \sin (\omega t + \dfrac{\pi}{2})$
- $V_C=V_{C0} \sin (\omega t \: – \dfrac{\pi}{2})$
です。
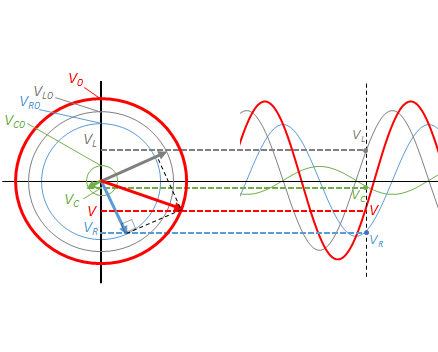
$\dfrac{\pi}{2}$ の位相のずれとは、参考円において互いに 90° の角度差をもっているということです。
したがって、参考円を考えると図のような等速円運動を考えればよいことになります。
その際に、各参考円の半径は各素子にかかる電圧の最大値となります。
これらのベクトルが図のように位相差を保ちながら、ぐるぐると回転している状態を想像してもらえばよいのです。（注：ここでの図における各電圧の大きさは適当です）
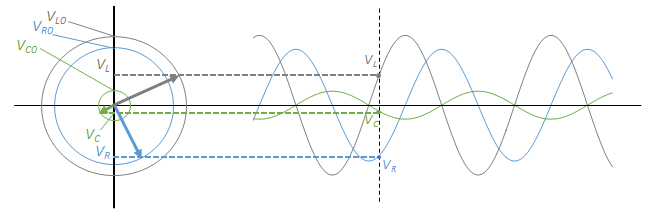
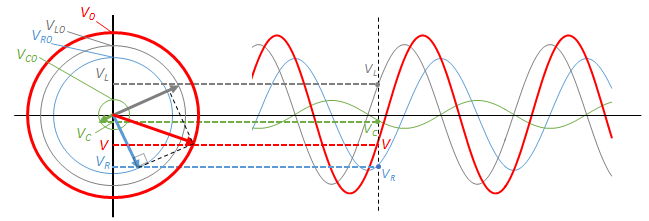
ここで、ある時刻 $t$ における回路全体の電圧を示すものは、参考円においてそれらを合成したもの（図の赤色の部分）に等しくなります。
$V=V_L+V_C+V_R$
インピーダンス
コイル $L$ とコンデンサー $C$ の位相差はちょうど $\pi$ です。
イメージをつかみやすくするために、回転して次の図のようになったときを考えます。
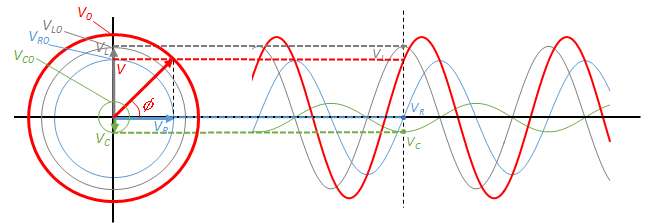
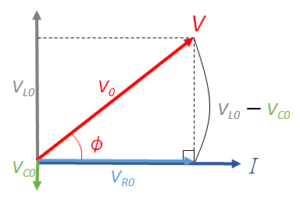
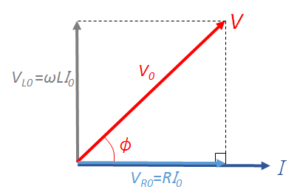
そうすると、求める $V$ の大きさは次の図において、
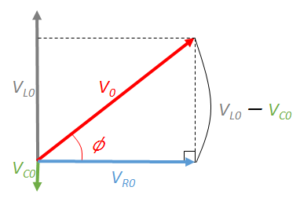
ピタゴラスの定理から
$V^2_{0}={V_{R0}}^2+(V_{L0 } \:- V_{C0})^2$
$V_{0}=\sqrt{{V_{R0}}^2+(V_{L0} \:- V_{C0})^2}$
さて、ここで各素子のオームの式
- $V_{R0}=RI_0$
- $V_{L0}=\omega LI_0$
- $V_{C0}=\dfrac{1}{\omega C}I_0$
であることから、これを $V_0$ の式へ代入します。（電流 $I$ は RLC に共通）
$V_{0}=\sqrt{{V_{R0}}^2+(V_{L0} \:- V_{C0})^2}$
$~~~~=\sqrt{(RI_0)^2 + \left( \omega LI_0 \:-\dfrac{1}{\omega C}I_0\right)^2 }$
$V_0=\sqrt{R^2 + \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }\:\:I_0$
実効値の場合も同様に、
- $V_{Re}=RI_e$
- $V_{Le}=\omega LI_e$
- $V_{Ce}=\dfrac{1}{\omega C}I_e$
- $V_{e}=\sqrt{{V_{Re}}^2+(V_{Le} \:- V_{Ce})^2}$
- $V_e=\sqrt{R^2 + \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }\:\:I_e$
ここで、 $\sqrt{R^2 + \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }=Z$ としてやります。
そうすると、
- $V_0=ZI_0$
- $V_e=ZI_e$
と書け、これはオームの式 $V=RI$ と同じ形です。
よって、この $Z$ を交流回路における抵抗をあらわす値と考え、$Z$ をインピーダンスと呼ぶことにします(単位 $\Omega$ )。
位相差
今回は、電流を $I=I_0 \sin \omega t $ としていましたが、回路全体にかかる電圧は電流との位相のずれを $\phi$ として、
$V=V_0\sin (\omega t + \phi) $ と考えられるということをお話しました。
電流の位相と抵抗の $V_{R}$ の位相は等しいため、図の角度 $\mathrm{\phi}$ が電流 $I$ に対する回路全体にかかる電圧 $V$ の位相のずれを示していることになります。
図では位相差を比較するために、
電流 $I$ と電圧 $V$ を同時に描いています。
よって、図から、RLC直列回路を流れる電流と回路全体にかかる電圧の位相差 $\phi$ は、
$\tan \phi = \dfrac{ V_{L0 }\:- V_{C0}\:}{V_{R0}}$
$~~~~~~~~~ = \dfrac{\:\omega L \:- \dfrac{1}{\omega C}\:}{R}$
となります。
$V_{R0}=RI_0$
$V_{L0}=\omega LI_0$
$V_{C0}=\dfrac{1}{\omega C}I_0$
を使いました。
注意：これらは RLC直列回路の式です。
LC直列回路 RC直列回路 RL直列回路
- LC直列回路
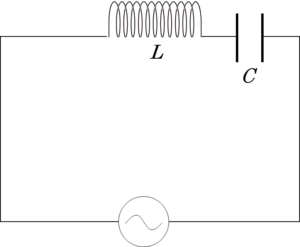
さて、RLC回路を考えてきましたが、例えば抵抗 $R$ がない場合はどうなるでしょうか。その場合は、単に式から抵抗に関する部分を消去します。（注：実際問題として回路の導線には抵抗があります）
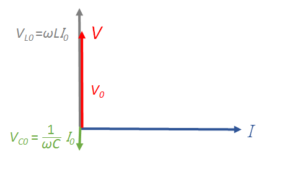
$Z=\sqrt{ \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }=\left |{\omega L \:-\dfrac{1}{\omega C}}\right |$
この場合の位相は、$\omega L$ と $\dfrac{1}{\omega C}$ の大きいほうを向きます。
もし $\omega L$ と $\dfrac{1}{\omega C}$ が同じ大きさのときはインピーダンス $Z$ が 0 になり、過大な電流が流れることになります。これは共振の記事で解説します。
同様に
- RC直列回路
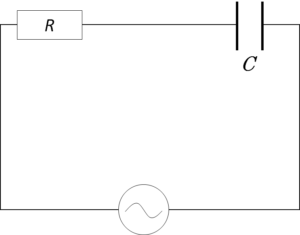
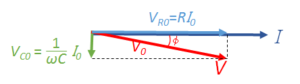
$Z=\sqrt{R^2 + \left(-\dfrac{1}{\omega C}\right)^2 }$
$\tan \phi = \dfrac{\:- \dfrac{1}{\omega C}\:}{R}$
- RL直列回路
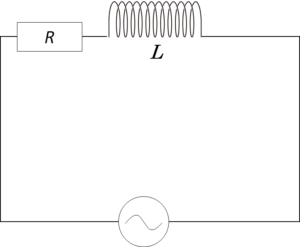
$Z=\sqrt{R^2 + \left(\omega L \right)^2 }$
$\tan \phi = \dfrac{\:\omega L \:}{R}$
まとめ
抵抗にかかる電圧 $V_R$ コイルにかかる電圧 $V_L$ コンデンサーにかかる電圧 $V_C$ とする。
各素子の最大値と実効値をそれぞれ以下の式で示す。
- 回路全体･･････最大値 $V_0$ 実効値 $V_e$
- 抵抗･･････････最大値 $V_{R0}$ 実効値 $V_{Re}$
- コイル････････最大値 $V_{L0}$ 実効値 $V_{Le}$
- コンデンサー･･最大値 $V_{C0}$ 実効値 $V_{Ce}$
RLC直列回路においては、回路に流れる電流を $I=I_0\sin \omega t$ とした場合、各素子にかかる電圧は
- $V_R=V_{R0} \sin \omega t$
- $V_L=V_{L0} \sin (\omega t + \dfrac{\pi}{2})$
- $V_C=V_{C0} \sin (\omega t \: – \dfrac{\pi}{2})$
- $V_{R0}=RI_0$
- $V_{L0}=\omega LI_0$
- $V_{C0}=\dfrac{1}{\omega C}I_0$
- $V_{Re}=RI_e$
- $V_{Le}=\omega LI_e$
- $V_{Ce}=\dfrac{1}{\omega C}I_e$
$V=V_L+V_C+V_R$
- $V_{0}=\sqrt{{V_{R0}}^2+(V_{L0} \:- V_{C0})^2}$
- $V_0=\sqrt{R^2 + \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }\:\:I_0$
- $V_{e}=\sqrt{{V_{Re}}^2+(V_{Le} \:- V_{Ce})^2}$
- $V_e=\sqrt{R^2 + \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }\:\:I_e$
$Z$ をインピーダンスという。
$V_0=ZI_0$
$V_e=ZI_e$
$Z=\sqrt{R^2 + \left(\omega L \:-\dfrac{1}{\omega C}\right)^2 }$
RLC直列回路を流れる電流と回路全体にかかる電圧の位相差 $\phi$ は、
$\tan \phi = \dfrac{\:\omega L \:- \dfrac{1}{\omega C}\:}{R}$
ながながと書きましたが、内容をしっかり理解すれば、実際問題覚えるべきことはそれほどありません。
次回
回路全体にかかる電圧 $V$ の、数学的計算による導出
RLC並列回路
コメント