コイル( 自己インダクタンス $L$ )に電流 $I$ が流れているとき、そのコイルには $U=\dfrac{1}{2}LI^2$ のエネルギーがたくわえられています。
コイルにたくわえられるエネルギー
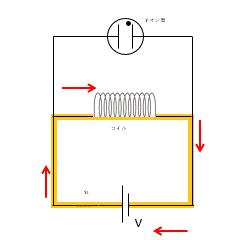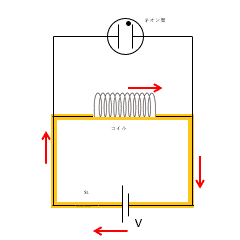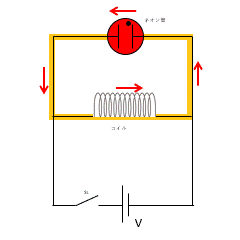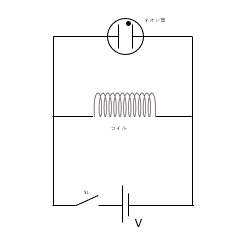
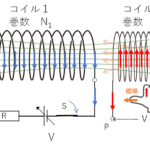
図ではネオン管とコイルを並列にして電源に接続しています。
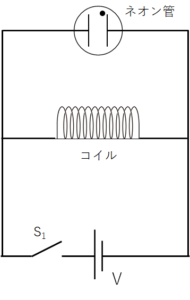
通常、ネオン管を点灯させるためには、6,000 ~ 15,000 V が必要です。
乾電池( 1.5 V )などを直接ネオン管につないでも点灯することはありません。
スイッチ $s_1$ をいれ、定常状態では図の黄色の回路に沿って電流が流れています。
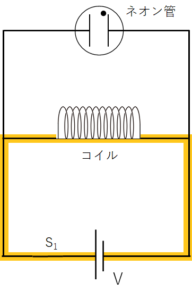
しかし、上図の回路でスイッチを切った瞬間に、一瞬だけネオン管の点灯を観察できるのです。
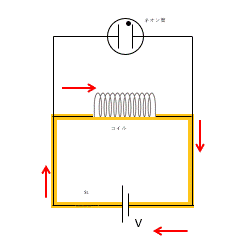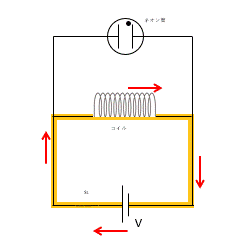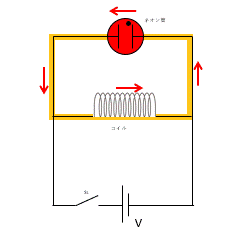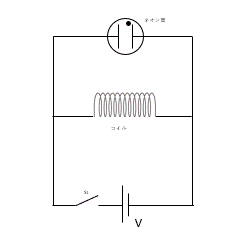
このとき、スイッチを突然切ったため、回路に流れていた電流が短時間のうちに 0 になろうとします。
しかし、コイルがあるため、コイルの自己誘導により電流を維持しようとします。
自己誘導の式
$V=-L\dfrac{\Delta I}{\Delta t}$
において、 $\Delta I$ が大きく、$\Delta t$ が非常に短いため、誘導起電力 $V$ が非常に大きくなり、ネオン管が一瞬点灯するというわけです。
ここで、コイルには電源はつながれていないので、ネオン管を一瞬点灯させるだけのエネルギーをコイルが持っていた、ということになります。
このように、電流が流れているコイルはエネルギー $U$ を蓄えていると考えられます。
コイルのエネルギー $U$
$U=\dfrac{1}{2}LI^2$
$L$:自己インダクタンス $I$:電流
解説
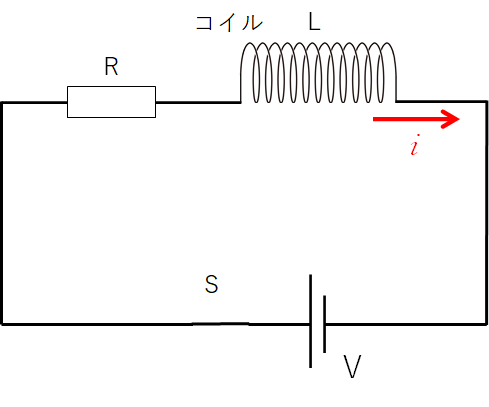
自己インダクタンス $L$ のコイルに、0 から $I$ まで電流を流したとします。
このとき、コイルにたくわえられるエネルギーを計算します。
コイルに流れる電流 $i$ を微小時間 $\Delta t $ で $i$ から $\Delta i$ だけ電流を変化させるとき、コイルは大きさ $V_L=L\dfrac{\Delta i}{\Delta t}$ の電圧を逆起電力として発生します。
そうすると、それにさからって、時間 $\Delta t $ で $\Delta i$ 変化させるために必要な仕事 $\Delta w$ は、 $w=qV$ で、時間 $\Delta t$ の間は $i$ と $V_L$ は一定とみなすと、
$\Delta w=\Delta q V_L$ ここで、 $i=\dfrac{\Delta q}{\Delta t}$ だから、
$~~~~~=(i\Delta t)V_L$ $V_L=L\dfrac{\Delta i}{\Delta t}$ を代入すると、
$~~~~~=i\Delta t \left( L\dfrac{\Delta i}{\Delta t} \right )=Li\Delta i$
今、$I$ の電流が流れているコイルが持つエネルギーは、電流が 0 から $I$ になるまでにコイルがされた仕事総和と考えられます。
よって、コイルの持つエネルギーは、この仕事について電流が 0 から $I$ まで足し合わせばよいことになります。
そこで、$\Delta i$ を $di$ と書き換えて $ 0 ~ I $ の範囲で積分します。
$$U=\int^I_0 Li\,d i =\dfrac{1}{2}LI^2$$
となり、コイルにたくわえられているエネルギーを求めることができました。
これは次のグラフの面積を求めていることと同じです。
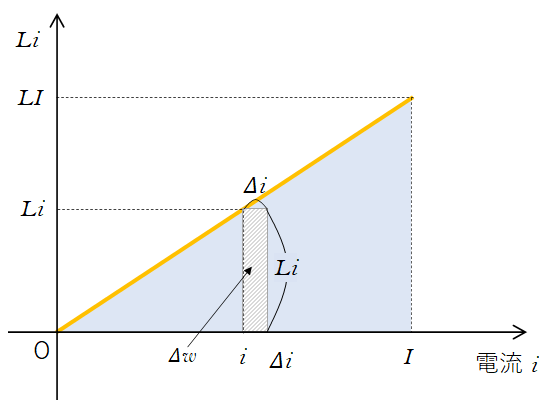
$\Delta w=Li\Delta i$
横軸が電流 $i$ であることに注意してください。

このグラフは 横軸が $i$ 、縦軸が $Li$ なのでコイルを流れる電流変化がどうであろうと必ず図のように直線になります。
これは、 $y=ax$ のグラフが、横軸 $x$ 、縦軸 $ax$ となり、直線となるのと同じです。




































コメント