- 第1宇宙速度 第一宇宙速度とは、次のような場合の速さです。 地球を質量 $M$、半径 $R$ の完全な球体とする。 地球半径 $R$ のところで周回する人工衛星の速さ $v_F$ を、第1宇宙速度と呼びます。 要するに、地球の地表面すれすれを飛ぶ人工衛星の速さのことです。 実際は空気抵抗もあるし、山や谷もあるので、そのような人工衛星はあり得ませんね。 ここでは遠心力を考えてみましょう。(運動方程式でも考えられます) 人工衛星には遠心力(慣性力)と重力が働いています。重力加速度 $g$ 人工衛星(質量 $m$ とする)から見ると、この二つはつり合っているため、次式が成り立ちます。 遠心力=重力 $m\dfrac{v_F^2}{R}=mg$ お気づきだと思いますが、 $ma=F$ として、運動方程式を考えても式の形は全く同じです。 より、 $v_F=\sqrt{gR}$ また、$GM=gR^2$ であるから、 $v_F=\sqrt{gR}=\sqrt{\dfrac{GM}{R}}$ です。これが地球表面上(半径 $R$ )を周回するための必要な速さ、第1宇宙速度です。 $GM=gR^2$ については、 (地球表面での重力)=(万有引力)より、 $mg=G\dfrac{mM}{R^2}$ で得られます。 万有引力の位置エネルギーについては、 万有引力と位置エネルギー重力に位置エネルギー mgh を考えるように、万有引力による位置エネルギーを考えることができます。 位置エネルギーはその基準位置を示す必要がありますが、基準位置は原則、任意の位置にとることができます。 万有引力による位置エネルギーを考えるときその基準位置は、一般には無限遠をとります。kokolainen.com を参照してください。 第2宇宙速度
- どれくらいの速さ?
第1宇宙速度
第一宇宙速度とは、次のような場合の速さです。
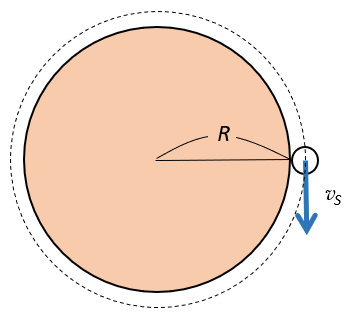
地球を質量 $M$、半径 $R$ の完全な球体とする。
地球半径 $R$ のところで周回する人工衛星の速さ $v_F$ を、第1宇宙速度と呼びます。
要するに、地球の地表面すれすれを飛ぶ人工衛星の速さのことです。
実際は空気抵抗もあるし、山や谷もあるので、そのような人工衛星はあり得ませんね。
ここでは遠心力を考えてみましょう。(運動方程式でも考えられます)
人工衛星には遠心力(慣性力)と重力が働いています。重力加速度 $g$
人工衛星(質量 $m$ とする)から見ると、この二つはつり合っているため、次式が成り立ちます。
遠心力=重力
$m\dfrac{v_F^2}{R}=mg$

お気づきだと思いますが、 $ma=F$
として、運動方程式を考えても式の形は全く同じです。
より、 $v_F=\sqrt{gR}$
また、$GM=gR^2$ であるから、
$v_F=\sqrt{gR}=\sqrt{\dfrac{GM}{R}}$
です。これが地球表面上(半径 $R$ )を周回するための必要な速さ、第1宇宙速度です。

$GM=gR^2$ については、
(地球表面での重力)=(万有引力)より、
$mg=G\dfrac{mM}{R^2}$ で得られます。
万有引力の位置エネルギーについては、
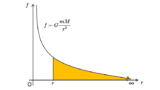
を参照してください。
第2宇宙速度
地球半径 $R$ のところで周回する人工衛星の速さ $v_F$ を、第1宇宙速度と呼びます。

人工衛星(質量 $m$ とする)から見ると、この二つはつり合っているため、次式が成り立ちます。

お気づきだと思いますが、 $ma=F$
として、運動方程式を考えても式の形は全く同じです。

$GM=gR^2$ については、
(地球表面での重力)=(万有引力)より、
$mg=G\dfrac{mM}{R^2}$ で得られます。
万有引力の位置エネルギーについては、

を参照してください。
第2宇宙速度とは、
地球表面からロケットを飛ばすとき、地球の重力圏を脱出するための最低速度のことです。
この場合のロケットは途中でエンジンを噴射しません。
最初の勢いで何とか乗り切ろう・・・という趣旨です。
実際のロケットは燃料とエンジンを積んでいますのでこのような初速度は必要ありません。
では求めてみましょう。
ここでは、万有引力による位置エネルギーを使った、力学的エネルギー保存則を用います。
また、第2宇宙速度を $v_S$ とします。
摩擦等のない場合、人工衛星のもつ力学的エネルギーは、いつも保存されます。
地球重力圏を脱出するということは、無限遠のかなたへ放っておいても飛んで行けるということを示します。
つまり、その場合、最小のエネルギーというのは、無限遠で ロケットの速さ=0 となる場合です。よろよろとなりながら無限遠にたどり着いた・・というイメージです。
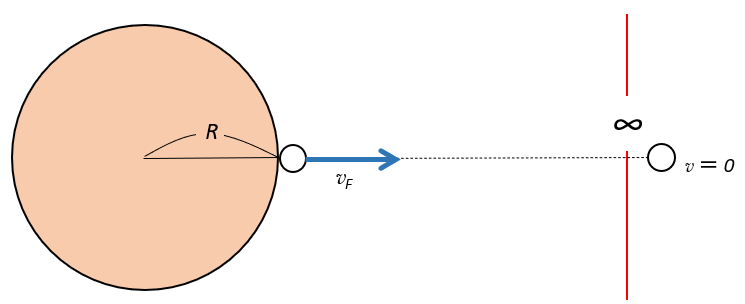
よって、 (力学的エネルギー)=(運動エネルギー)+(位置エネルギー)=一定 から
地球半径 $R$、地球質量 $M$、重力加速度 $g$、ロケット質量 $m$、第2宇宙速度 $v_S$、万有引力定数 $G$ とすると、
(地球表面での力学的エネルギー)=(無限のかなたでの力学的エネルギー)
より
\begin{eqnarray}
\dfrac{1}{2}mv_S^2+\left( -G\dfrac{mM}{R} \right)&=&\dfrac{1}{2}m0^2+\left( -G\dfrac{mM}{\infty}\right)\\\\
&=&0+0\\\\
\end{eqnarray}
より、$v_S=\sqrt{\dfrac{2GM}{R}}$ を得ます。
第1宇宙速度の時と同様に 、$GM=gR^2$ を代入すると、
$v_S=\sqrt{\dfrac{2GM}{R}}=\sqrt{2gR}$
です。
万有引力による位置エネルギーの基準を $\infty$ にしたので計算が楽ですね。

つまり第1宇宙速度の $\sqrt{2}$ 倍です。
ん、意外と小さいんだな・・・?
無限という言葉が出るので、
もっと大きい速度が必要と思ってしまいました。
万有引力は距離 $r^2$ に反比例するので、
早く減衰するからでしょう。
どれくらいの速さ?
第1宇宙速度と第2宇宙速度がどれくらいか計算してみましょう。
地球半径はだいたい $6400\:\mathrm{km}$ です。
簡単のため、重力加速度を $g\fallingdotseq 10\:\mathrm{m/s^2}$ としましょう ^_^。
そうすると、第1宇宙速度 $v_F$ と第2宇宙速度 $v_S$ は、
$v_F=\sqrt{gR}=\sqrt{10\times 6400\times 10^3}=8000\:m/s=8.0\:\mathrm{km/s}$
$v_S=\sqrt{\dfrac{2GM}{R}}=\sqrt{2}v_F \fallingdotseq 11200\:\mathrm{m/s}=11\:\mathrm{km/s}$
ですね。($g=9.8$ で計算すると、$v_F\fallingdotseq 7.9 \mathrm{km/s}$、$v_S \fallingdotseq \mathrm{11.2 km/s}$)
第1宇宙速度では 1 秒間で約 $8\:\mathrm{km}$ 進みます。
地球1周 $40000\:\mathrm{km}$ とすると、地球表面上を飛ぶ人工衛星は、$5000 \:\mathrm{s}$ 、約1時間24分で地球を1周します。
逆に、この速さがないと、地球表面上を飛ぶ人工衛星にはなりません。




































コメント