ガウスの法則
ガウスの法則として知られている式
$$N=4\pi k Q$$
これは、電荷 $Q$ から出ている電気力線総本数 $N$ を示しています。
（$k$ はクーロンの法則の比例定数）
電気力線は非常に有用で、あなたの電場イメージを作るのに最適です。
そして、ガウスの法則を用いることで、イメージから数式へと導くことができ非常に便利なのです。
今回はこの式を導いてみましょう。
ガウスの法則
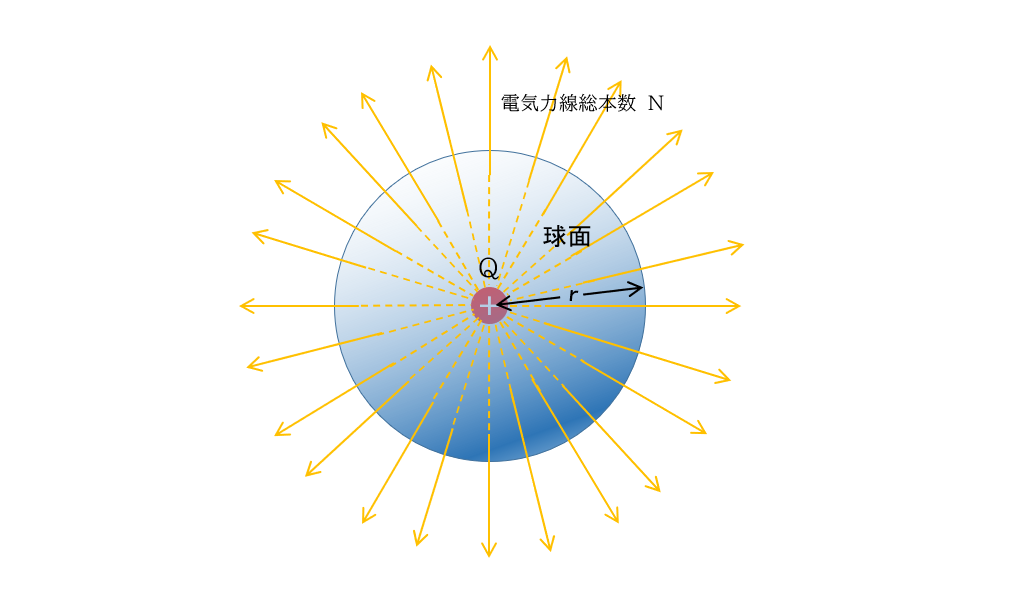
では次の図を見てください。
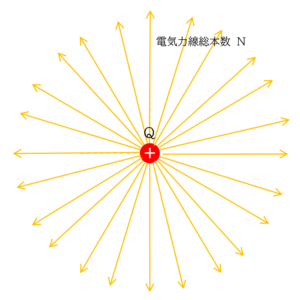
電荷 $Q$ から電気力線が放射状に出ています。
この場合、等方性からいって、電気力線はどの方向にも3次元的に等しく出ていると考えられます。
さて、この電気力線をすべて数えたい！ とします。
どうすればよいでしょうか？
ここでよいアイデアがあります。
電荷 $Q$ のまわりを仮想的な球で覆ってしまうのです。
次の図のようなイメージになります。
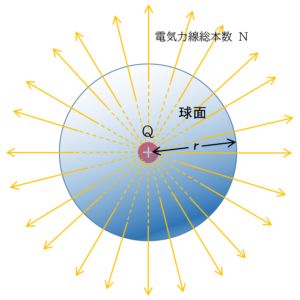
この図では電荷 $Q$ のまわりに半径 $r$ の球をイメージしています。
実際にこういう球を置く、ということではありません。あくまでイメージです。
したがって、実際の電場に影響を与えることはありません。念のため。
電気力線の性質として、電気力線は、途中で増減したり枝分かれすることはありません。
よって、この球を貫く電気力線を全て数えれば、それは電荷 $Q$ から出る電気力線総本数 $N$ に等しくなります
つまり、間接的な方法で電荷 $Q$ から出る電気力線を数えよう、というわけです。
では、そのためにまず、球面上での電場の強さ $E$ を求めていきましょう。今、完全な球体で電荷 $Q$ から同じ距離 $r$ に球面があるとすると、球面上での電場の強さ $E$ は球の表面上では、どこでも等しくなります。
また、電場ベクトルは球の中心から放射状にでてているため、電場の方向は球面に対して垂直です。
球面上の電場の強さは、電場を求める式から、
$E=k\dfrac{Q}{r^2}$
となります。
強さ $E$ の電場ですから、定義からこの球面上では、$1\:[m^2]$ あたり $E=k\dfrac{Q}{r^2}$ 本の電気力線を引きます。
ここで電気力線の定義を思い出しましょう
電気力線は、電場の強さ $E\:[N/c]$ では $E\:[本/m^2]$ 引くと約束したものです。
詳細については次の記事
このとき、この球面を貫く電気力線総本数を数えれば、それが電荷 $Q$ から出る電気力線総本数 $N$ に等しくなるのでした。
そして、いま球面には $1\:[m^2]$ あたり $E=k\dfrac{Q}{r^2}$ 本の電気力線があるのですから、総本数 $N$ は球表面（面積 $S$ ）では、$E\times S$ で示されます。（球の面積 $S$ は、$S=4\pi r^2$ です）
すなわち、
\begin{eqnarray}
N&=&E\times S\\\\
&=&\left(k\dfrac{Q}{r^2}\right)(4\pi r^2)\\\\
&=&4\pi kQ
\end{eqnarray}
となります。
ここで、誘電率 $\varepsilon$ を使って書くと、$k=\dfrac{1}{4\pi \varepsilon}$ なので、
$$N=4\pi kQ=\dfrac{Q}{\varepsilon}$$
となります。
問題
電気力線の良いところは、以前の記事でも示しましたが、イメージがしやすいこと。
また、電気力線本数を数えることでその場の電場の強さを求めることができる点です。
「ガウスの法則」、しっかり理解しておきましょう。
基本をきちんと理解できれば、見たことがない問題が出た時も対処できる可能性が大きくなります。
以下で電気力線を使って「物理のエッセンス」の電磁気 7 番の問題を考えていますのでご参考に！
コメント