ホール効果

ホール効果

ホール効果とは、導体や半導体に電流を流し、磁場をかけたときに導体内部で電位差を生じる現象です

導体や半導体に磁場をかけることで、内部を運動する電子などのキャリアにローレンツ力がかかります。
そのため、導体内部ではキャリアの偏りが生じて、電位差を生じます。
この現象をホール効果といい、この電位差をホール電圧といいます。

キャリアが電子の場合

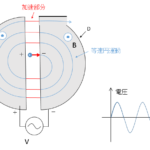
図では、キャリアが電子（電荷 $e$ ）の場合を示しています。
図の下から上に向かって、磁場 $B$ がかけられています。

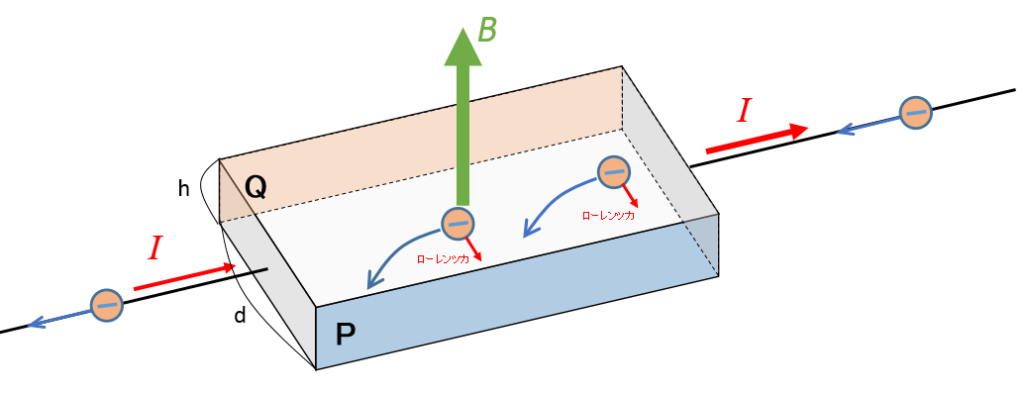
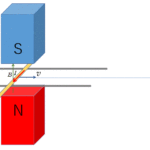
このとき、導体内部では電流方向とは反対方向に電子が速さ $v$ で運動しているとします。
そうすると、図の場合、電子は P 面に向かうローレンツ力を受けて曲がります。

したがって、P 面付近には次第に負電荷である電子が増加することになり、導体内部では Q から P に向かう電場 $E$ が形成されます。

この電場 $E$ が十分大きくなると、P 面へ向かうローレンツ力と Q 面へ向かう電場から受ける力がつり合うため、電子が直進する定常状態になります。（下図）

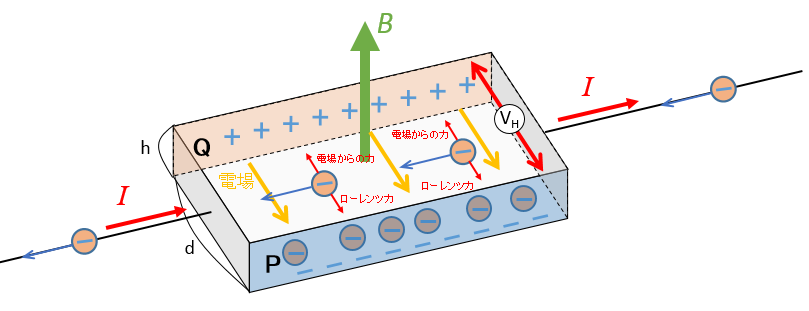
ということは、ローレンツ力 $evB$ と電場 $E$ からの力 $eE$ がつり合うため、

$evB=eE$　　です。よって、

$E=vB\:\:\cdots (1)$　　　　　となります。

ここで、電流 $I$ の式　$I=envS$　より、（$S$ は導体の断面積　$S=hd$   $h$,$d$ は図参照）

$v=\dfrac{I}{enS}=\dfrac{I}{enhd}\:\:\cdots (2)$　　です。

PQ間のホール電圧 $V_H$ は、PQ間の電場の大きさ $E$ とPQ間の距離 $d$ から、

$V_H=Ed$　　ですから、さきほどの式 $E=vB\:\:\cdots (1)$　より、

$V_H=vBd$

これに　$v=\dfrac{I}{enhd}\:\:\cdots (2)$　を代入すると、

$V_H=\dfrac{I}{enhd}\cdot Bd=\dfrac{IB}{enh}$

となります。次式のように変形すると、

$n=\dfrac{IB}{nhV_H}$

これにより、$V_H,\:I,\:B,\:h$ を測定すれば、導体中の電子密度 $n$ が計算できます。

キャリアが正孔（ホール）の場合

正孔（ホール）は $+$ の電荷（電気量 $e$ ）と同様に扱います。
したがって、図のようなP面に向かう方向にローレンツ力を受けて、P 面付近に正電荷（電気量 $e$ ）が多くなるというイメージです。

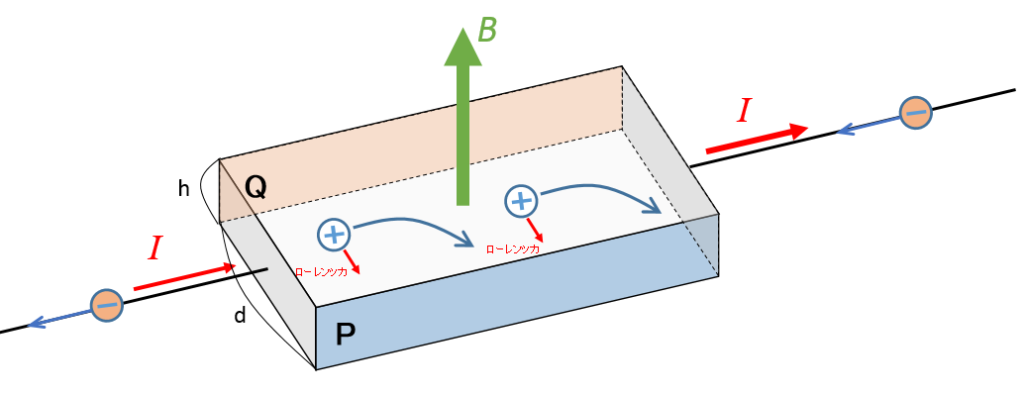
そのため、PからQの方向に電場形成され、正孔(ホール）は電場方向に力を受けることになります。
定常状態になれば、ローレンツ力と電場からの力がつり合うことにより、正孔は直進します。（下図）

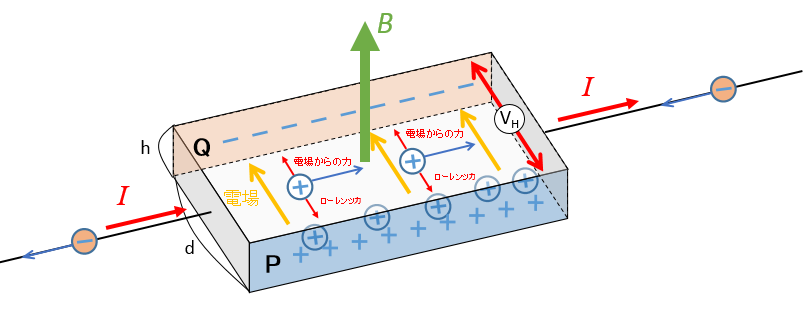
キャリアが電子でも正孔でもホール効果に関する式は同じになります。
ただし、P面とQ面の電荷は異なるため、観測されるホール電圧は、キャリアが電子の場合とは正負が逆になります。
したがって、試料のキャリアが電子か正孔かは、PQ間の電位を調べることで判定できます。

ちなみに
ここでいう正孔（ホール）とは、hole つまり穴のことです。
ホール効果・Hall effect のHall は人名です。
エドウィン・ホール（Edwin Herbert Hall, 1855-1938）