波動でよく出る言葉に「位相」があります。
教科書の説明を読むと「媒質の振動状態を示す量」とされていますが、何のことか良くわかりませんね。
波動で波長 $\lambda$ 離れていると位相は $2\pi$ [rad]、半波長離れていると $\pi$ [rad] 違うというのはどのように理解すればよいのでしょうか。
悩んでいる人に、実際にたずねてみても、あいまいなことが多いようです。
私が解説するとすれば、位相とはズバリ「参考円の回転角」です。
参考円とは何かについてはここ。
今回はこの位相についてわかりやすく解説します。
いまさら聞けない位相
単振動・等速円運動と波動
波の伝播
波動を伝える媒質の各点は単振動しています。
その単振動がずれて伝播した結果、全体として波が移動しているように見えるのです。

サッカー場でよくやるウェーブでは人は立ったり座ったりするだけです。
すなわち、隣の人が立てば立ち、そして座ります。
単振動(立ったり座ったり)がずれて伝わった結果、ウェーブが移動するように見えると考えられます。
そして、物理学において、媒質が単振動している様子を記述するのは「等速円運動」です。
つまり、波動は単振動で示され、単振動は等速円運動で示される。
つまり、波動 ← 単振動 ← 等速円運動 というわけですね。

媒質の単振動
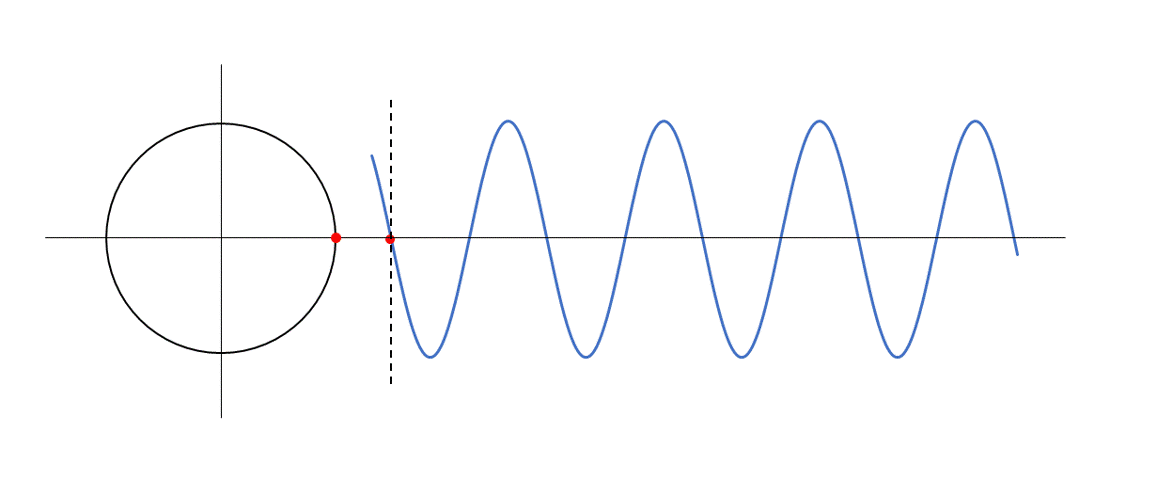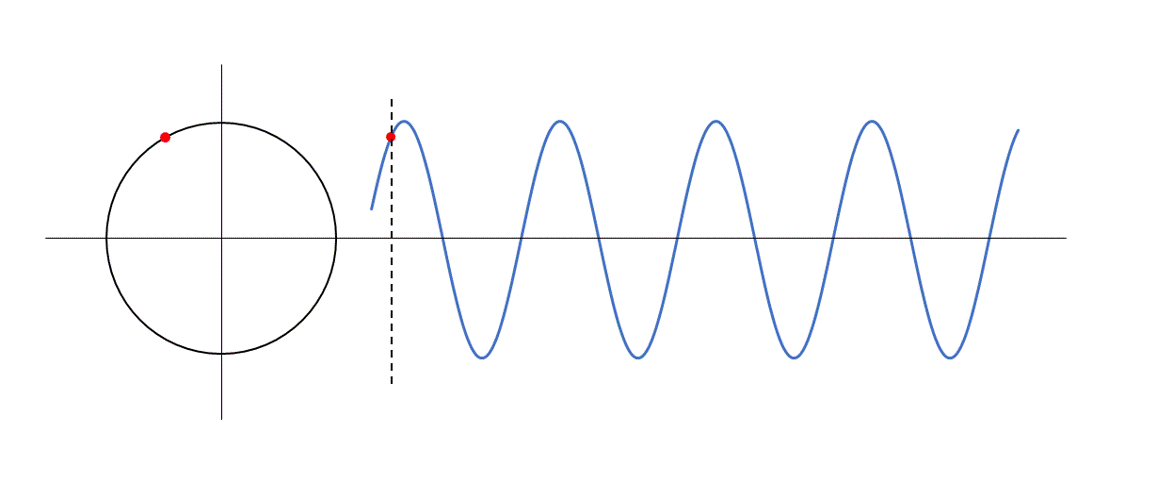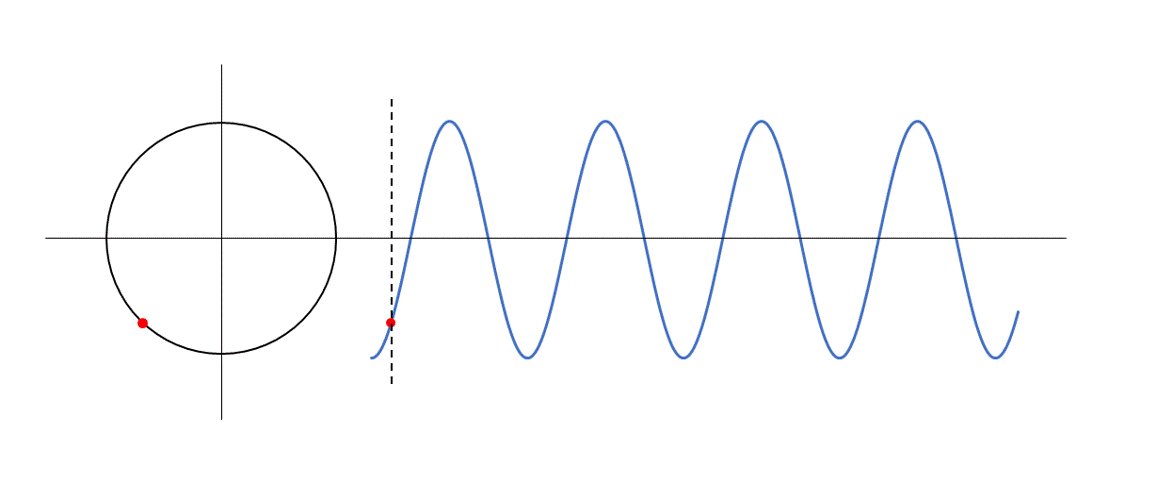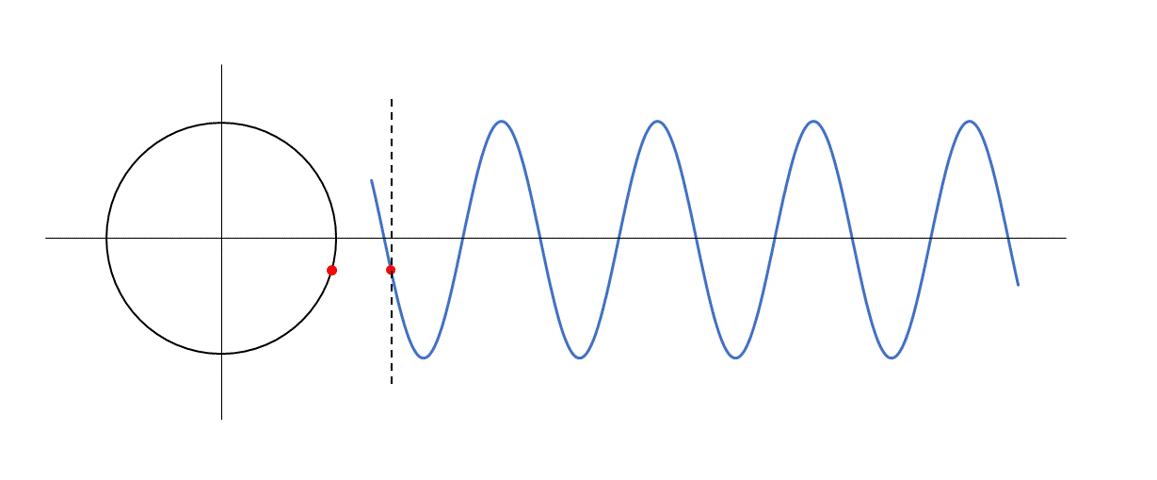
波動において媒質の各点が単振動してます。このとき、ある点について、その媒質の単振動している様子を示す等速円運動を考えます。
次の図の波動上の赤い点が単振動しています。
その単振動の参考円上の対応する赤い点は等速円運動していることがわかりますね。
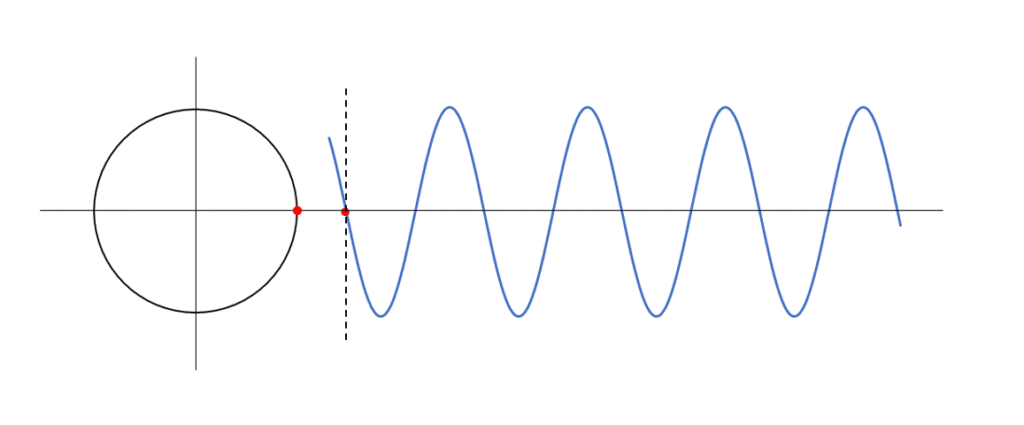
このとき、この等速円運動の円を参考円と名付けることにします。
このとき、参考円における回転角のことが位相です。
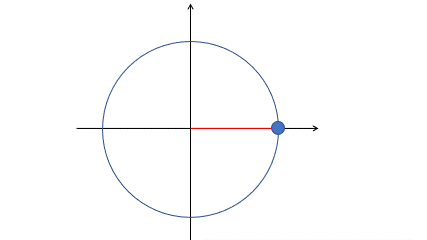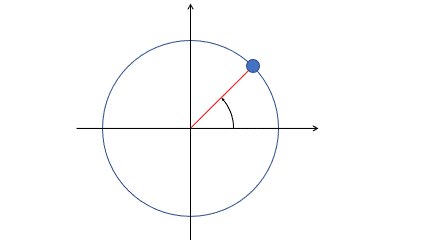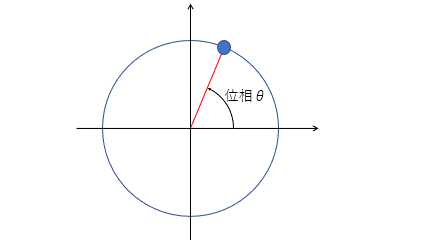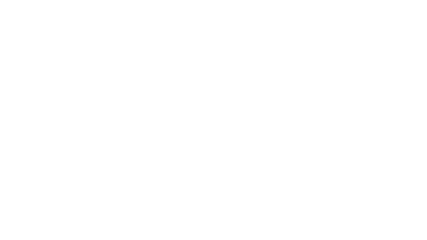
進行波では媒質の位相は常に変化しています。
同位相と逆位相
ここまで理解できれば、波動の同位相と逆位相はどれになるかカンタンにわかるはずです。
よくある説明のように波の、山と谷は逆位相どうし ・・・・ とうのは確かにそうですが、何も山や谷に限ったことではないのがお分かりでしょう。
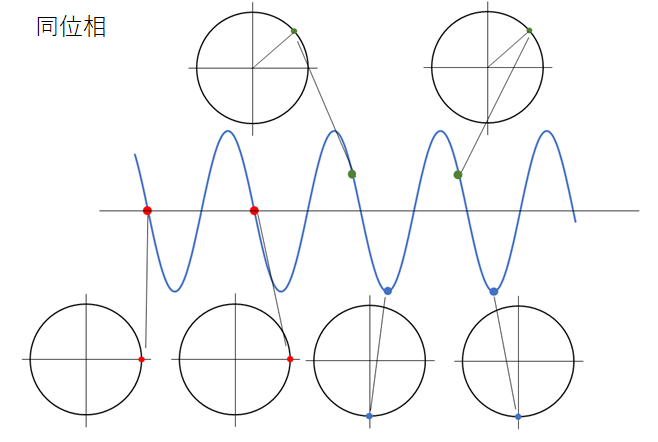
同位相
参考円における角度が同じものが同位相
参考円上の位置が同じ、といったイメージでもよいでしょう。
このとき波動上ではちょうど1波長 $\lambda$ 離れています。
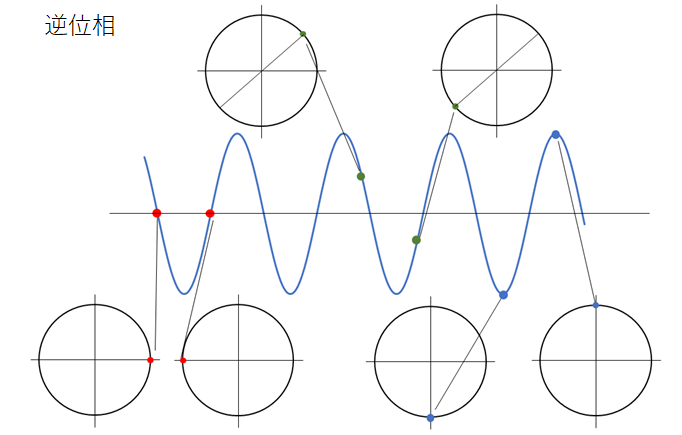
逆位相
参考円における角度がちょうど反対側( $\pi$ ラジアン ・・・ 180°)にあるものが逆位相です。
参考円上の位置が反対側のものどうし、といったイメージです。
このとき波動上ではちょうど半波長 $\frac{\lambda}{2}$ 離れています。(図を一部修正しました)
したがって、あらゆる媒質の点にはその状態の同位相、逆位相の状態が考えられます。




































コメント