アンペールの法則と磁場
電流と磁場の関係については次の記事を参照してください。
アンペールの法則
アンペールの法則を高校物理風に解説すると、
ある導線に流れる電流が $I$ とするとき、その導線を囲む閉じた線にそって $1\:\mathrm{Wb}$ の磁極を動かすときの磁場がする($1\:\mathrm{Wb}$ あたりの)仕事 $w$ と電流 $I$ は等しい。
$I\:\mathrm{[A]}=\dfrac{w\:\mathrm{[J]}}{1\:\mathrm{[Wb]}}=w \:\mathrm{[J/Wb]}$
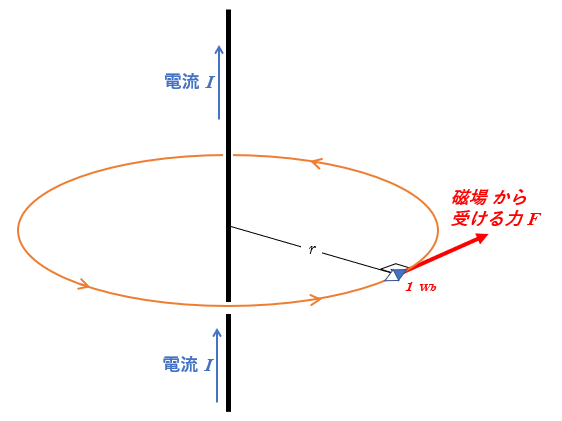
このときの導線を囲む閉じた線分は、どのような経路や形をしていても基本的にはOKです。
これは、磁場から受ける力が保存力であることを示しています。
直線電流と磁場
無限に長い直線状の導線を考えます。
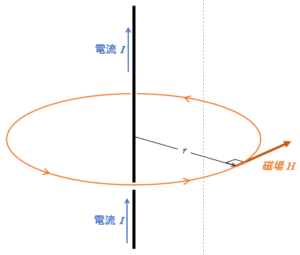

アンペールの法則ではどのような閉じた線分を考えてもいいのですが、ここでは計算のしやすい円を考えます。
円に沿う場合は、磁場の大きさが常に一定だと考えられます。
導線から距離 $r$ のところに $m=1\:\mathrm{Wb}$ の磁極を置き、半径 $r$ の閉じた円周に沿って導線の周りを1周 $(距離:x)$ させるために必要な($1\:\mathrm{Wb}$ あたりの)仕事 $w$ は
$w=Fx=(mH)x=(1\times H)\times (2\pi r)$
となります。(ここで $F=mH$ を使った)
この仕事が $I$ に等しいわけだから
$w=I=(1\times H)\times (2\pi r)$
より、
$H=\dfrac{I}{2\pi r}$
を得ます。
円形電流の磁場
次の図にあるような円形の導線が、その円の中心に作る磁場について。
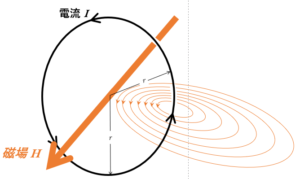
磁場の大きさを求める場合、考え方としては、同じように、$1\:\mathrm{Wb}$ を1周させるときの仕事を求めるということでいいはずですが、この場合1周に沿う磁場Hが一定ではないため、(簡単には)できません。
この磁場を求めるのは、ビオサバールの法則を使えば可能ですが、ここでは触れません。
ソレノイド内部の磁場
アンペールの法則を使って、ソレノイド内部の磁場についても簡単に求めることができます。
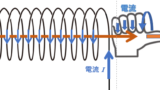
次の図は、ソレノイドの断面を示しています。
ここで、このソレノイドを作る導線を囲む、図に示すような閉じた四角形の線分を考えましょう。

どのような閉じた線分を考えてもよいわけですから、一番簡単に計算できる形を選びます。
四角形のソレノイドと平行な長さを $l$ とします。
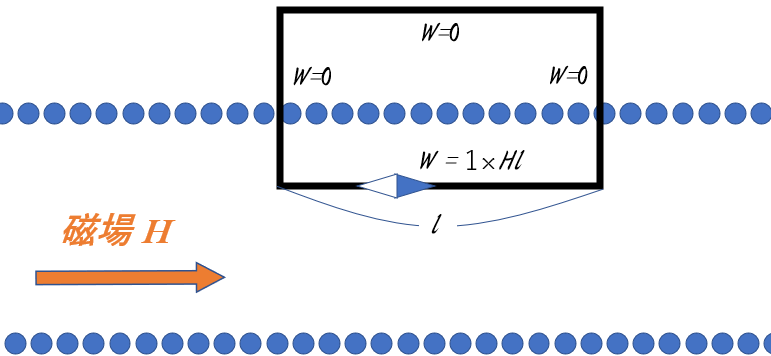
理想的な無限に長いソレノイドは外部磁場が 0 としてよいことに注意します。
また、ソレノイドを直角に横切る線分部分では、磁場からの力は運動方向に垂直であるため、仕事は 0 であることに注意してください。
したがって、ソレノイド内部のソレノイドと平行の線分部分だけが、$1\:\mathrm{Wb}$ の磁極を運ぶのに仕事が必要になります。(図の $l$ の部分)
そのときの仕事 $w$ は、アンペールの法則より
$w=I=Fx=(mH)x=(1\times H)\times l$
ソレノイドの場合は、導線は1本ではなく、多数本集まっているので、今考えた四角形の $l$ の間にある導線の数を $N$ とすると、一本の導線を流れる電流値 $i$ を考えた場合、
$I=N \times i=H\times l$
です。
したがって、
$H=\dfrac{N}{l}i$
ここで、$n=\dfrac{N}{l}$ として、$n\:\mathrm{[本/m]}$ を $1\:\mathrm{m}$ あたりの巻き数、と定義すると、
$H=ni$
が導かれます。
これから、ソレノイド内部の磁場は、ソレノイド半径の大きさに無関係であることがわかります。




































コメント