気柱共鳴の実験

気柱共鳴の実験

気柱共鳴で解説したように、気柱に生じる定常波から波長 $\lambda$ を計算することができます。

また、音速 $V$ は、$V=331.5+0.6t$ （$t$ ：気温）から計算できますから、波長と音速から　$V=f\lambda$　より、振動数 $f$ を計算することができます。

では実際によく行われる実験を通して、気柱計算における注意点を解説していきます。

実験装置

気柱共鳴実験装置は図のようなもので、左側の水だめを上下させることで水面の高さ（気柱の長さ）を自在に変えることができます。

この気柱の上部で音叉などを鳴らして、管内に定常を作り出します。

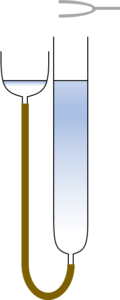
定常波

管の上部で音叉をたたくと、その音波が気柱内で共鳴・共振して定常波を作ります。
定常波は閉端で節、開端で腹を作ります。

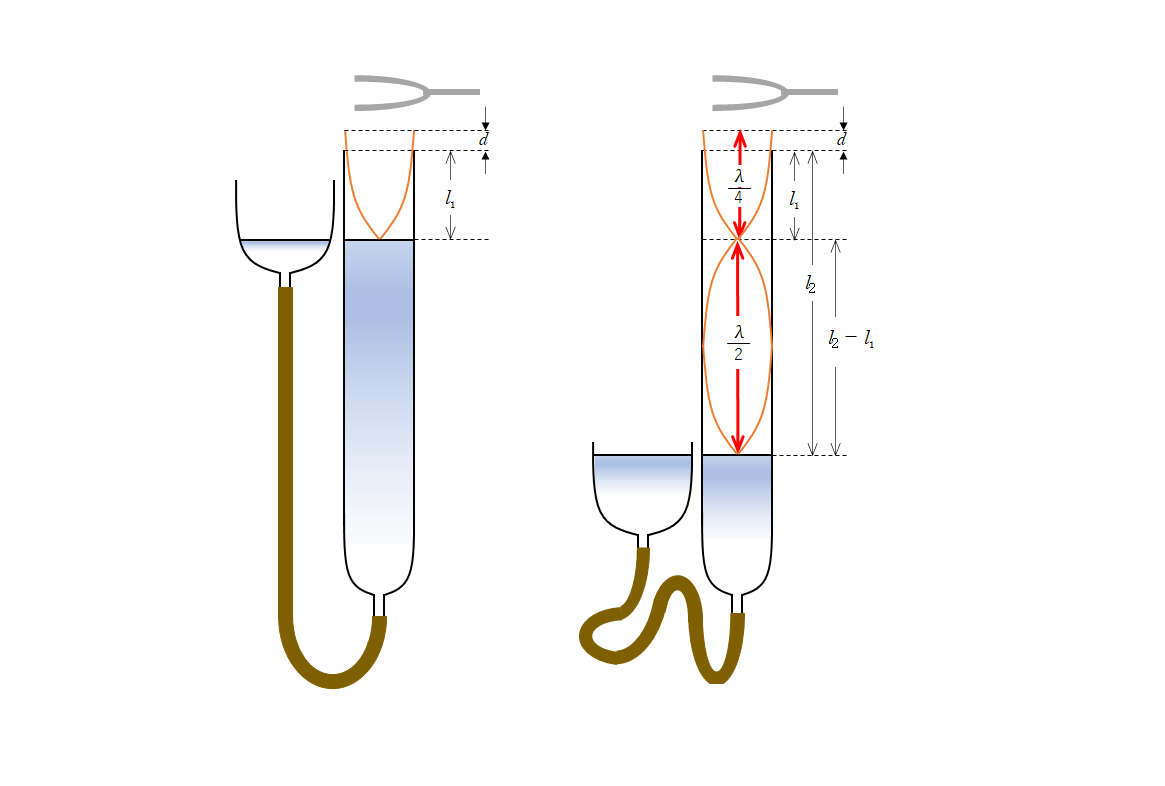
よって、水面を上端から少しずつ下げていって最初に共鳴が生じる点（大きく聞こえる）では次の図のような状態と考えられます。

実際に実験をすると、

共鳴点では意外なほど大きな音が聞こえて

驚く人も多いんですよ。

このとき、定常波の上端は気柱上部に少しはみ出る形になります。

これを開口端補正と呼びます。開口端補正についてはこちらを参照してください。

したがって、$\lambda$ を求めたいとき、上の図で $l_1$ を $\dfrac{\lambda}{4}$ とすると誤差が大きくなってしまいます。

そこで次のようにします。

同じ音叉を用いて、最初の共鳴点からさらに水面を下げていくと、2度目の共鳴点が観測できます。
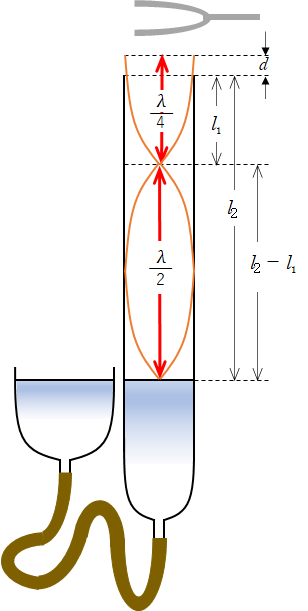
そのとき、気柱内の定常波は次の図のような状態だと考えられます。

ここで、一度目に共鳴したところの気柱上端からの距離 $l_1$ と2度目のときの距離 $l_2$ から次の式が導かれます。

$l_2 \: – \: l_1 =\dfrac{\lambda}{2} $

このようにして差をとると、上端で生じているはずの開口端補正 $d$ をキャンセルすることができます。

したがって、

$\lambda = 2(l_2 \: – \: l_1)$

$f = \dfrac{V}{\lambda} = \dfrac{V}{ 2(l_2 \: – \: l_1)}$

開口端補正

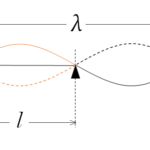
開口端補正 $d$ は下の図から

$\dfrac{\lambda}{4} = l_1 + d$

より得られます。