ポアソンの法則
ポアソンの法則
理想気体では、断熱変化するときの圧力 $p$ と体積 $V$ には、$pV^{\gamma}$ ＝ 一定、という関係がある
この $\gamma$ は比熱比と呼ばれ、$\gamma=\dfrac{C_p}{C_V}$ の関係があります。
気体の法則 ボイル・シャルルの法則 や 状態方程式については
を見てください！
定圧モル比熱 $C_p$ と定積モル比熱 $C_V$ については
以前の記事を参照してください。
このポアソンの法則について、高校物理の教科書を見ると、高等学校の範囲外？ということかな、説明がはぶかれ、天下り的に式が示されています。
なんだか気になりませんか？
ここでは、できるだけ天下り的ではない説明を試みました。
では、さっそく式を導出します。
式の導出
気体が、圧力 $p$、体積 $V$、絶対温度 $T$、モル数 $n$ だとします。（図 左）
この状態方程式は、$pV=nRT$ と示されます。（$R$：気体定数）
その状態から断熱変化をして、圧力 $p+\Delta p$、体積 $V+\Delta V$、絶対温度 $T+\Delta T$ へと微小変化したとします。（図 右）
そうすると、状態方程式は、$(p+\Delta p)(V+\Delta V)=nR(T+\Delta T)$ と書くことができます。（モル数 $n$ は変化なし）
これを展開してみると
\begin{eqnarray}
(p+\Delta p)(V+\Delta V)&=&nR(T+\Delta T)\\\\
pV+p\Delta V+\Delta pV+\Delta p \Delta V&=&nRT+nR\Delta T\\\\
\end{eqnarray}
ここで、$pV=nRT$ と、微小量であることを考えて、$\Delta p \Delta V=0$ とすると、
\begin{eqnarray}
pV+p\Delta V+\Delta pV+\Delta p \Delta V&=&nRT+nR\Delta T\\\\
p\Delta V+\Delta pV&=&nR\Delta T\\\\
\end{eqnarray}
となります。
さて、ここで断熱過程であることから、熱力学第1法則より、$Q=\Delta U+W’$ において $Q=0$ なので、
$0=\Delta U+W’$
です。ただし、$W’$ は気体のする仕事です。
考えている過程が、断熱過程であるので、気体圧力は一定ではありませんね。
したがって、一般に $W’=p\Delta V$ ではないが、このとき微小変化を考えていますから、$\Delta V$ の微小範囲においては圧力は一定としてよく、 $W’=p\Delta V$ となります。（気になる人は補足へ）
ゆえに、
$0=\Delta U+W’=\Delta U+p\Delta V$
となります。
さらに、定積モル比熱 $C_V$ を用いると、$\Delta U=nC_V\Delta T$ であるから、（参考記事：定積モル比熱はいつでも使える）
\begin{eqnarray}
0&=&\Delta U+W’\\\\
&=&\Delta U+p\Delta V\\\\
0&=&nC_V\Delta T+p\Delta V
\end{eqnarray}
より、$\Delta T=-\dfrac{p\Delta V}{nC_V}$
これを、$p\Delta V+\Delta pV=nR\Delta T$ へ代入します。
\begin{eqnarray}
p\Delta V+\Delta pV&=&nR\Delta T\\\\
p\Delta V+\Delta pV&=&nR\left(-\dfrac{p\Delta V}{nC_V}\right)\\\\
\Delta pV&=&-p\Delta V-R\left(\dfrac{p\Delta V}{C_V}\right)\\\\
\Delta pV&=&-p\Delta V\{1+\left(\dfrac{R}{C_V}\right)\}\\\\
\Delta pV&=&-p\Delta V\dfrac{C_V+R}{C_V}\\\\
\end{eqnarray}
ここで、マイヤーの関係式 $C_p=C_V+R$ を代入します。
そうすると、 $C_V+R=C_p$ であるから、
\begin{eqnarray}
\Delta pV&=&-p\Delta V\dfrac{C_V+R}{C_V}\\\\
\Delta pV&=&-p\Delta V\dfrac{C_P}{C_V}\\\\
\end{eqnarray}
この両辺を $pV$で割ることにします。
\begin{eqnarray}
\dfrac{\Delta pV}{pV}&=&\dfrac{-p\Delta V\dfrac{C_P}{C_V}}{pV}\\\\
\dfrac{\Delta p}{p}&=&-\dfrac{\Delta V\dfrac{C_P}{C_V}}{V}\\\\
\end{eqnarray}
ここで、右辺に現れた $\dfrac{C_p}{C_V}$ を特別な量として $\gamma =\dfrac{C_p}{C_V}$ としましょう。
この $\gamma$ を比熱比と呼ぶことにします。
そうすると、
\begin{eqnarray}
\dfrac{\Delta p}{p}&=&-\gamma \dfrac{\Delta V}{V}\\\\
\end{eqnarray}
今まで微小変化を考えてきましたが、$\Delta$ を$d$ と書き換え、足し合わせるため、$\int$ します。
そうすることで、圧力や体積が微小変化だけではない場合を考えることができます。
\begin{eqnarray}
\int{\dfrac{d p}{p}}&=&-\int{\gamma \dfrac{d V}{V}}\\\\
\end{eqnarray}
$\int{\dfrac{dx}{x}}=\log {x} +C$ ですから、同様に、
\begin{eqnarray}
\int{\dfrac{d p}{p}}&=&-\int{\gamma \dfrac{d V}{V}}\\\\
\log{p}&=&-\gamma \log{V}+C\:\:\:\:(C:定数 \:\:\:\: \gamma\log V=\log V^{\gamma}) \\\\
\log{p}+\log{V^{\gamma }}&=&C\\\\
\log{pV^{\gamma}}&=&C\\\\
pV^{\gamma}&=&e^C=k\:\:\:\:(k:定数)
\end{eqnarray}
よって、$pV^{\gamma}=一定 $ となるわけです。
ここで、$\dfrac{pV}{T}=k\:\:(一定)$ を用いると、$p=\dfrac{T}{V}k$ を代入して、
$$ pV^{\gamma}=\dfrac{T}{V}kV^{\gamma}=TV^{\gamma-1}=一定 $$
より、$TV^{\gamma-1}=一定$ も成り立ちます。
これらが理想気体の断熱変化における、圧-力 $p$ と、体積 $V$、絶対温度 $T$ の関係式となります。
ただし、微小量 $\Delta p$、$\Delta V$ を考えたので、準静的な変化（変化がつながっている）であることを前提としていることに注意してください。
よく演示実験でやるような、「どかん」というような急激な変化ではありません（どんなんだ？）。
$p-V$ グラフ
では断熱変化のグラフを描いてみましょう。
このとき、等温変化のグラフとの違いに気をつけて描いてみると次の図のようになります。補足参照
等温曲線どうしは交わることはありませんが、等温曲線と断熱曲線は交わります。
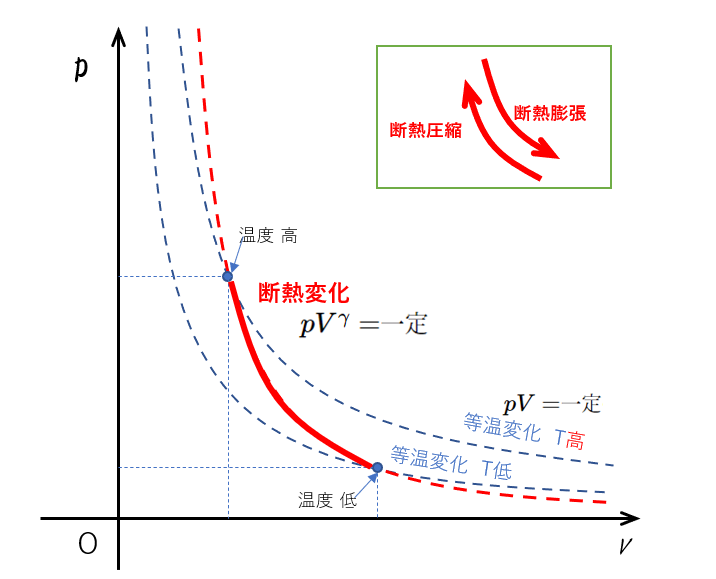
なぜならマイヤーの関係（$C_p=C_V+R $）から、$C_P>C_V$ より、$\gamma=\dfrac{C_p}{C_V}>1$ ですね。
ちょっと変形してやると、$pV^{\gamma}=C$ では、$p=\dfrac{C}{V^{\gamma}}$ とできますね。
これは、$y=\dfrac{k}{x^n}$ のグラフを描くことと同じです。（$n>1$、$k$ 定数）
つまり、$V$ が大きくなるほど $p$ は小さくなる（$V$ が小さくなるほど $p$ は大きくなる）ため、グラフはアルファベットの「L」または、ひらがなの「し」のような形になります。（ちょっと違うか・・）
これを見ると、等温変化との比較から、
- 断熱圧縮の場合、気体温度が上昇
- 断熱膨張時では、気体温度が降下
することが明らかです。
補足 微小変化
注意：どうしても気になる人のために、
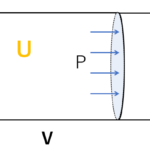
図において、$W’$を求めましょう。ただし、$\Delta p$ は微小量とします。
$W’$ は、図の囲まれた台形面積を求めればよいと近似できます。
では、台形面積を計算しましょう。
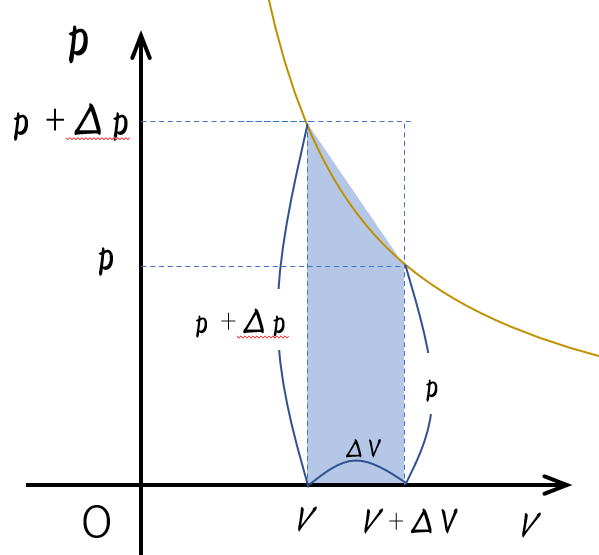
\begin{eqnarray}
W’&=&(上底＋下底）\times 高さ \div 2\\\\
&=&(p+p+\Delta P)\times \Delta V \div 2\\\\
&=&p\Delta V+\dfrac{1}{2}\Delta p \Delta V\\\\
\end{eqnarray}
このとき、微小量同士の掛け算 $\Delta p \Delta V$ は $0$ とみなせます。
したがって、微小量を考えるとき、$W’=p\Delta V$ は成り立つといえます。
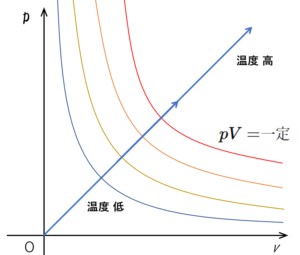
補足 p-V図での温度分布
注意：等温変化のグラフは、$\dfrac{pV}{T}=一定$ より、温度 $T$ が一定であれば、$pV=一定$のグラフになるから、図のようになり、グラフの右上に行くほど高温となります。
コメント