ローレンツ力

ローレンツ力

ローレンツ力とは、運動する荷電粒子が磁場からうける力のことです

フレミングの法則で出てきた、導線にはたらく力はどこからきているのでしょうか？
ここではその原因として、導体中の電子にはたらく力（ローレンツ力）を考えてみます。

普通は、フレミングの力がはたらくのは導体だけです。たとえば、木の棒を磁場中においても影響を受けることはありません。

また、フレミングの力がはたらくのは導体に電流が流れている場合に限ります。

このように考えると、電流の担い手である運動する電子が磁場から力を受け、その総和がフレミングの力となってあらわれていると考えられます。

電子に限らず、運動する荷電粒子は磁場から力を受け、それをローレンツ力と呼びます。
その際に正電荷と負電荷ではローレンツ力が働く向きが逆になります。

ローレンツ力 $f$ の大きさは、電荷 $q$ の物体が速さ $v$ で、磁場 $B$ 中を運動する場合に、次の式で示されます。

$f=qvB$

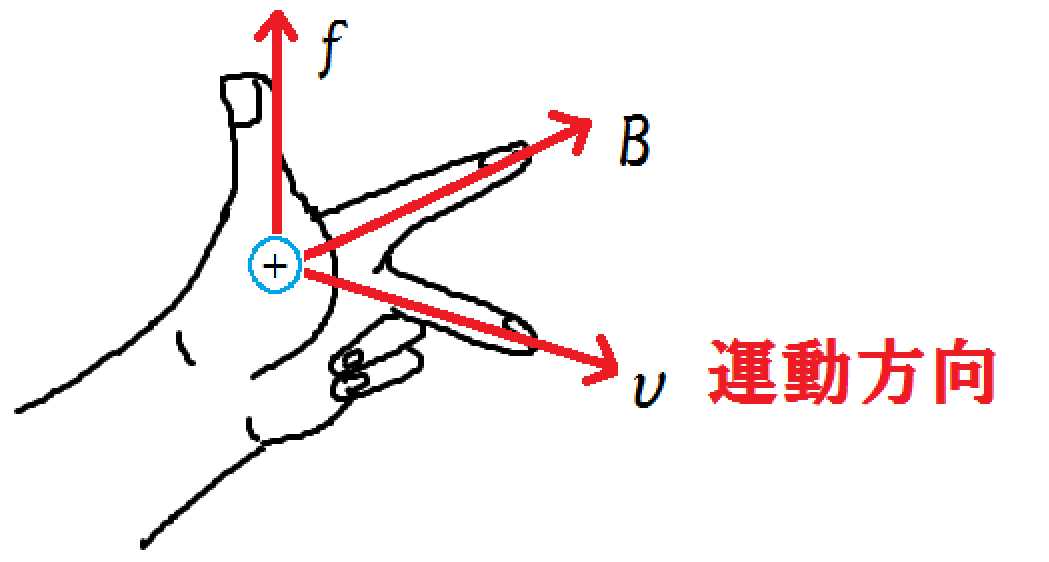
このときの力の向きはローレンツの左手則を使って考えますが、力の方向は、電荷の正負により変わってくるので要注意です。

荷電粒子が正のとき

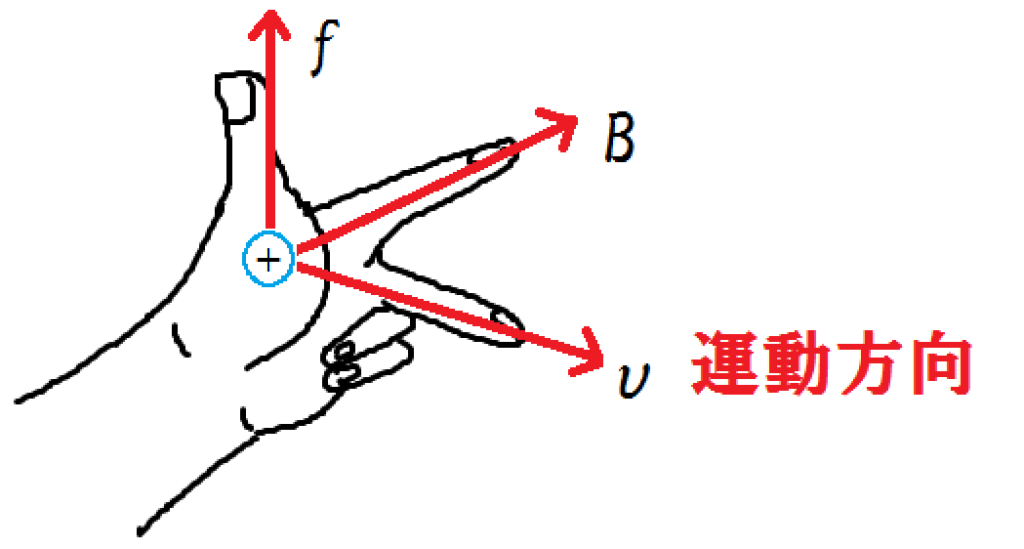
荷電粒子の運動する向きをそのまま、中指の向きに一致させます。
そのとき、図のように左手の指をかまえるとき、親指の向きがローレンツ力の向きと一致します。

ローレンツ力を受ける荷電粒子の運動

ローレンツ力は荷電粒子に対して仕事をしない。よってエネルギーは増減しない。 磁場に垂直に進入した場合は、荷電粒子は等速円運動をし、その周期は荷電粒子の速さに無関係である。 磁場に斜めに進入した場合は、螺旋（らせん）運動をおこなう。

kokolainen.com

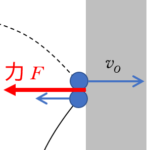
荷電粒子が負のとき

荷電粒子が負のとき　⇒　荷電粒子の運動方向を逆向きにとります。
（$-$ の電荷を持つ粒子が飛ぶ方向と、電流向きは反対向きのため）

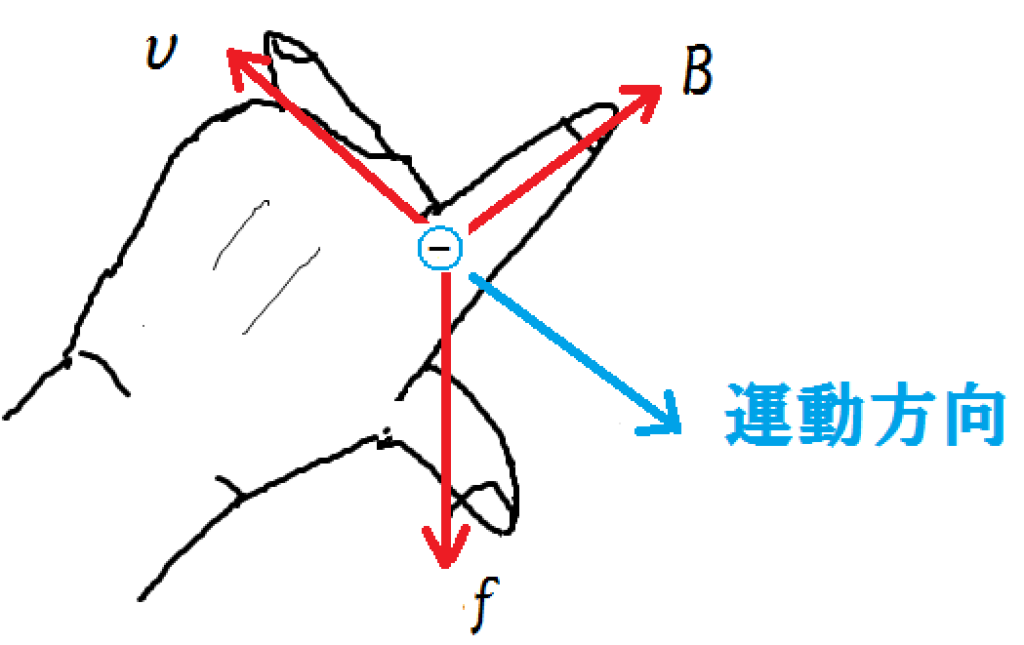
ということは、電子が運動しているときは、その運動方向を逆向きになるようにしなければなりません。
（注：中指の向きを電子の運動の向きに合わせて、親指と逆向きにローレンツ力をとってもかまいません）

ちなみに、電子の電荷の大きさを $e$ とすると、ローレンツ力は　$f=evB$　です。

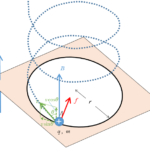
以上、荷電粒子が正負いずれの場合でも注意すべきは、荷電粒子の運動方向 $v$ と磁場 $B$ 、ローレンツ力 $f$ は互いに直交していることです。

もし直交していないときは、直交する成分を考えれば OK です。

フレミングの力からローレンツ力を求めてみる

磁束密度 $B$ の磁場の中に、磁場に対して垂直におかれた導線（長さ $l$ ）について考えます。

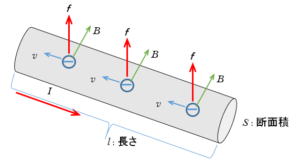
このとき、フレミングの力の大きさは、 $F=IBl$　でした。（⇒ フレミングの左手の法則）

この導線の長さ $l$ 中に、$N$ 個の電子があるとし、電子密度(注1)を $n$  、導線の断面積 $S$ 、電子の運動の速さ $v$ 、電子の電荷の大きさ $e$ とします。

そうすると、電子1個にはたらく力 $f$ は、$F$ を、総数 $N$ で割ればよいから、

$f=\dfrac{F}{N}$　　　　　　ここで $F=IBl$ を代入します。

$~~~=\dfrac{IBl}{N}$　　　　　また、$I=envS$　（⇒ I=envS の式）を代入すると、

$~~~=\dfrac{(envS)Bl}{N}$　　　電子の数 $N$ は、 $N=nSl$　と示されるので(注2)、

$~~~=\dfrac{(envS)Bl}{nSl}$

$f=evB$

となり、磁場が電子1個に及ぼす力 $f=evB$ を求めることができました。

よって、一般にローレンツ力の大きさは、電荷の電気量の大きさを $q$ として、次の式で示されます。

$f=qvB$

(注1) 電子密度とは、一般に、$[個/m^3]$ で示され、単位体積中にある電子の数を示します。

(注2) 長さ $l$ 、断面積 $S$ の導体の体積は $Sl$ であり、電子の密度が $n$ であるから、その中の電子の総数 $N$ は、 $N=nSl$　で示される。