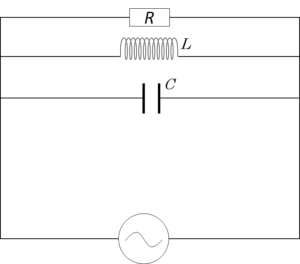
RLC並列共振で解説したように、固有周波数 ( 共振周波数 ) $f_0$ ( 周期 $T$ ) 、コイルインダクタンス $L$ 、コンデンサー電気容量 $C$ で、
$f_0=\dfrac{1}{2\pi\sqrt{LC}}$
$T=2\pi \sqrt{LC}$
のとき、コイルとコンデンサーが作る閉回路で振動電流が流れます。
この現象を電気振動とよびます。
また、電気振動ではエネルギー保存則から、コイルとコンデンサーのつくる閉回路を流れる電流 $I$ 、コンデンサーの電圧 $V$ とすると、
$\dfrac{1}{2}LI^2 + \dfrac{1}{2}CV^2 =\: 一定$
が成り立っています。ここで、電流の最大値 $I_0$ 、コンデンサーの電圧の最大値 $V_0$ とすると、
$\dfrac{1}{2}LI^2 + \dfrac{1}{2}CV^2 = \dfrac{1}{2}L{I_0}^2 = \dfrac{1}{2}C{V_0}^2 $
電磁気の記事は次を参照してください。
電気振動 交流の基礎9
RLC並列共振
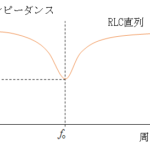
RLC並列回路において、共振周波数 $f_0$ で共振している場合、図のコイルとコンデンサーの合成インピーダンスは $\infty$ です（RLC並列回路 交流の基礎6）。したがって、電源からの電流はコイルとコンデンサーには流れません。
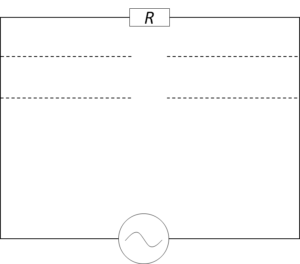
つまり、この回路においては全体から見ると、
コイルとコンデンサーは断線しているよう見えます。
実際は、共振しているRLC並列回路において、コイルとコンデンサーのつくる閉回路内にはいったりきたり振動する電流が流れています。これが電気振動です。
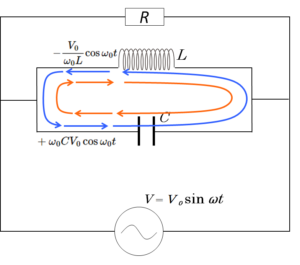
これは一度振動が起これば、電源を取り外しても継続します。
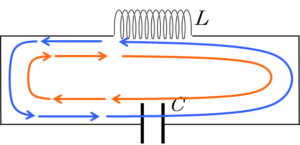
振動電流について
なぜ、コイルとコンデンサーのつくる閉回路には振動電流が流れているのか考えてみます。
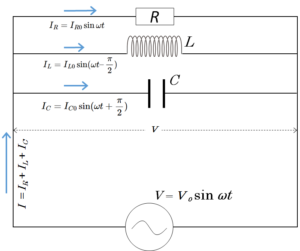
コイルにかかる電圧は $V=V_0\sin\omega t$ で、コイルに流れる電流 $I_L$ （ 位相の遅れ $\dfrac{\pi}{2}$ ）は、コイルリアクタンスが $\omega L$ だから、コイルに流れる電流は次の計算式で示されるはずです。
$I_L= I_{L0} \sin \left(\omega t – \dfrac{\pi}{2} \right)= -\dfrac{V_0}{\omega L}\cos \omega t$
( $I_{L0} = \dfrac{V_{L0}}{\omega L}=\dfrac{V_{0}}{\omega L}$ 注：並列のため $V_{L0}=V_{C0}=V_0$ )
同様に、コンデンサーにかかる電圧は $V=V_0\sin\omega t$ で、コンデンサーを流れる電流 $I_C$ （ 位相は $\dfrac{\pi}{2}$ 進む ）は、コンデンサーリアクタンスが $\dfrac{1}{\omega C}$ だから、次の計算式で示されます。
$I_C=I_{C0} \sin \left(\omega t + \dfrac{\pi}{2} \right)= +\: \omega CV_0\cos \omega t$
( $I_{C0} = \omega C V_{C0} =\omega CV_0$ 注：並列のため $V_{L0}=V_{C0}=V_0$ )
ここでこれらの電流の和を取ります。
$I_L+I_C = -\dfrac{V_0}{\omega L}\cos \omega t + \omega CV_0\cos \omega t$
$~~~~~~~~~~~~~= \left( \omega C \: – \dfrac{1}{\omega L} \right) V_0\cos \omega t$
共振している場合、閉回路外部から電流は流れ込まず・流れ出ない、のですから、これらの電流は相殺されて 0 になります。
したがって、共振角周波数 $\omega_0$ 共振周波数 $f_0$ として、
$\left( \omega_0 C \: – \dfrac{1}{\omega_0 L} \right)＝0$
$\omega_0 =\dfrac{1}{\sqrt{LC}}$
$f_0 = \dfrac{\omega_0}{2\pi} = \dfrac{1}{2\pi\sqrt{LC}}$
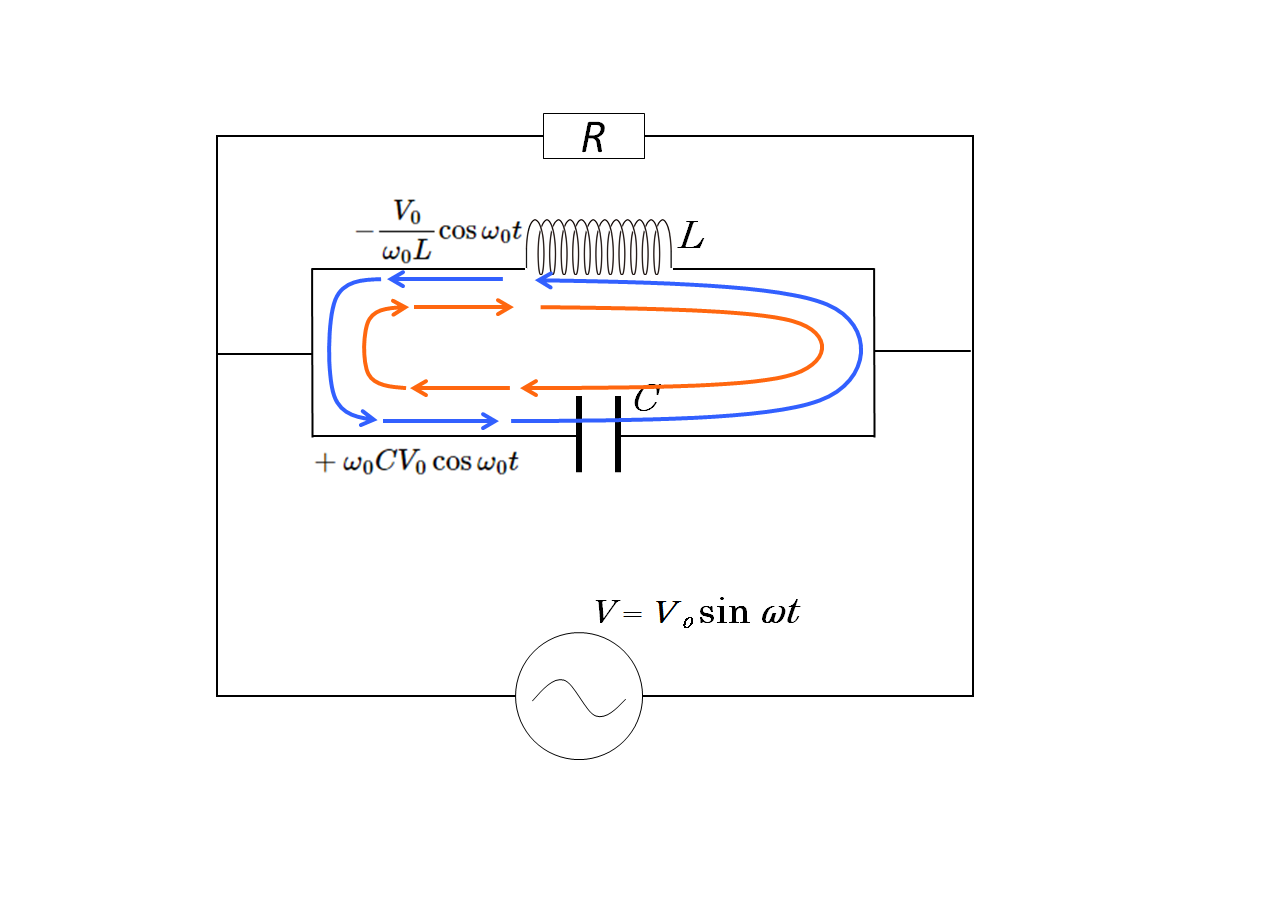
この場合、次の図のようにコイルとコンデンサーを流れる電流は逆を向きます。
つまり、コイルとコンデンサーの電流はそれぞれ位相が $\pi$ 違うため、それらの大きさが同じとき、合成すると 0 になり、電流はLCの閉回路から流れ出なく・流れ込まないというわけです。
したがって、電源電圧が共振周波数 $f_0$ のとき、コイルとコンデンサーの作る閉回路内では振動する電流が流れます。
振動していれば、この状況はたとえ電源をとっても同じであるため、LCの閉回路だけでも振動することになります。
このときの共振周波数 $f_0$ を、電気振動では固有周波数と呼び、振動周期を $T$ とすると、
$T=\dfrac{1}{f}=2\pi \sqrt{LC}$
電気振動のエネルギー
コイルとコンデンサーでは電力を消費しない。よって導線の抵抗が無視できるとき、このコイルとコンデンサーのつくる閉回路内ではエネルギー保存則が成り立ちます。
すなわち、コイルのエネルギー $\dfrac{1}{2}LI^2$ コンデンサーのエネルギー $\dfrac{1}{2}CV^2$ を足したものは保存され、（実際は導線に抵抗があるため次第に減衰します）
$\dfrac{1}{2}LI^2 + \dfrac{1}{2}CV^2 = 一定 $
コンデンサーに最大電圧 $V_0$ がかかる瞬間は、電荷はすべてコンデンサー極板上にあります。よって、閉回路を流れる電流は 0 です。
また、コンデンサーの極板上の電荷が 0 で、コンデンサーの極板間電圧が 0 の瞬間は、全ての電荷は導線上を流れています。よって、閉回路では最大の電流 $I_0$ が流れています。
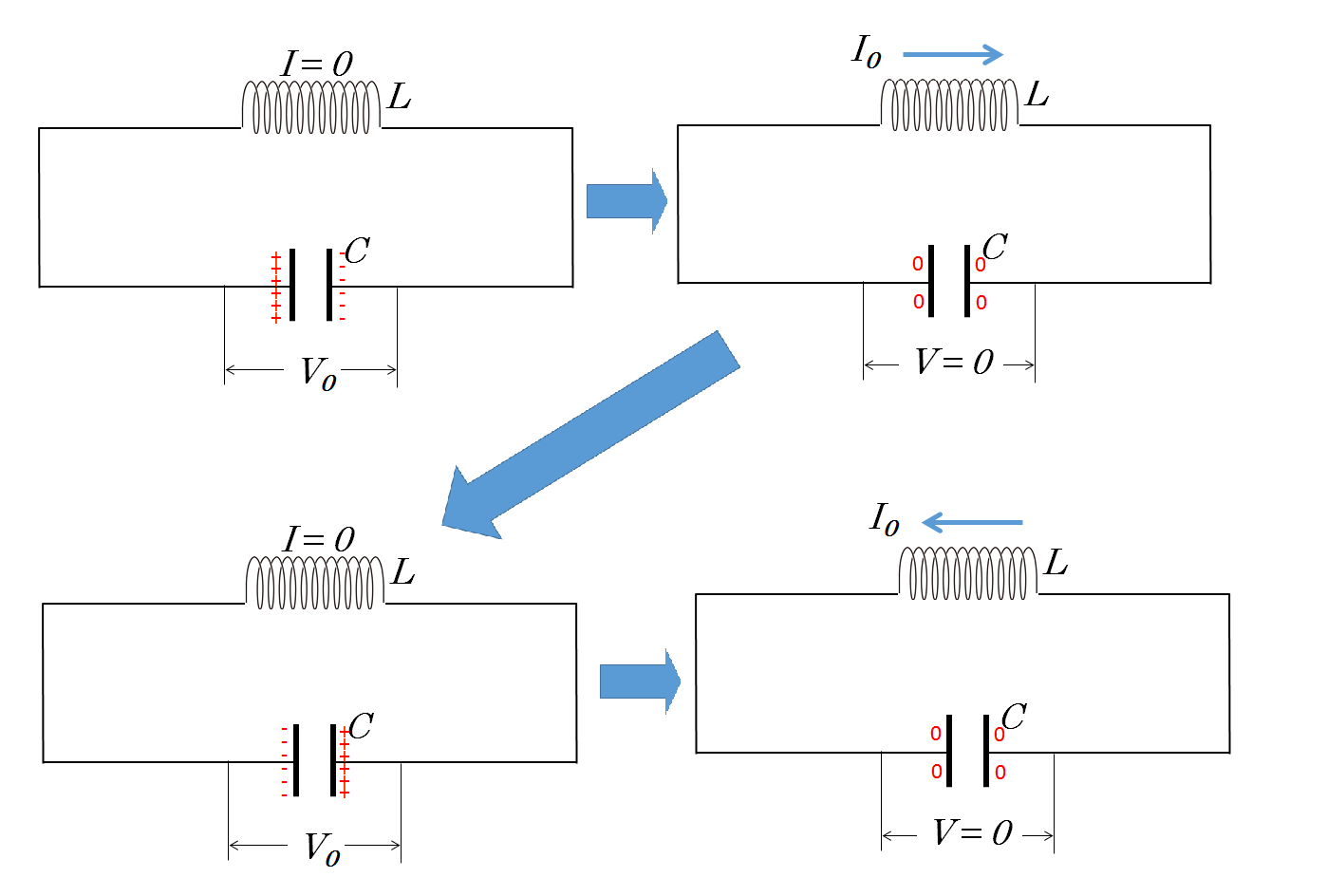
したがって、
$\dfrac{1}{2}LI^2 + \dfrac{1}{2}CV^2 =\dfrac{1}{2}L{I_0}^2 + 0 = 0 + + \dfrac{1}{2}C{V_0}^2一定 $
のエネルギー保存則が成り立ちます。
コメント