運動量保存則
運動量と力積
運動量と力積についての詳しい記事はこちらへ
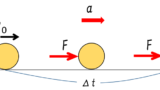
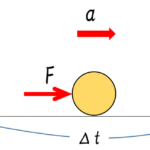
質量 $m$ 、速度 $\vec{v_0}$ の物体が力 $\vec{F}$ を時間 $\Delta t$ の間だけ受けて速度が $\vec{v}$ へ変化する場合、
$m\vec{v_0}+\vec{F}\Delta t=m\vec{v}$
が成り立ちます。
つまり、 最初の運動量+力積=最後の運動量 です。
このとき、 質量×速度 $m\vec{v}$ を、運動量、 力×時間 $\vec{F}\Delta t$ を力積と呼びます。
運動量と力積は物理学上、とても重要な概念です。
運動量保存則
質量 $m_A$ と $m_B$ の二つの物体が一直線上で衝突する場合を考えましょう。

図にあるように外部から力を受けることなく、質量 $m_A$ 速度 $v_A$ の物体が、質量 $m_B$ 速度 $v_B$ の物体に一直線上で衝突し、速度がそれぞれ $v_A’$ 、 $v_B’$ になった場合を考えます。
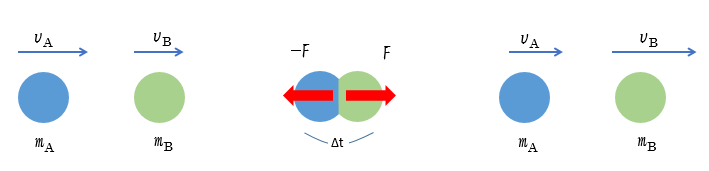
このとき、2物体が接触する時間 $\Delta t$ 、及ぼしあう力を $F$ とします。
作用反作用の法則により、2物体が接触する時に及ぼしあう力は物体 A 、B ともに同じ大きさで一直線上反対向きです。
物体AB、それぞれについて運動量と力積の式を立ててみます。
$m_Av_A+F\Delta t=m_A’v_A’\:\:\cdots\cdot(1)$
$m_Bv_B+(-F\Delta t)=m_B’v_B’\:\:\cdots\cdot(2)$
これらの式を辺々足します。
$(1)+(2)$
\begin{eqnarray}
m_Av_A+m_Bv_B&=&m_Av_A’+m_Bv_B’
\end{eqnarray}
この得られた式は、衝突の前後での系の運動量総和が増えも減りもしないことを示しています。
つまり、これが運動量保存則です。

系とは、
「考える範囲」のことだと考えてもいいでしょう
運動量保存則は、作用反作用の法則が成り立っているからこそ成立するわけで、その意味では作用反作用の法則そのものを示しています。
また、作用反作用の法則においては、お互いが及ぼしあう力は、全く同等であり、よくある誤解のように「力を受けたから、力を及ぼす」のような「仕返し」のようなものではありません。
作用反作用の法則により、物体ABは全く同時に同じ力を及ぼしあうのです。
そこにタイムラグはありません。
それが力が作用するという意味なのです。
そうでないとこの保存法則は成り立ちません。

だからこそ、ニュートンの時代の 万有引力は不思議なものだったわけです。
なぜなら、作用反作用を適用すれば、遠く離れた天体同士が空間を隔てて、瞬時に力を及ぼし合う・・・ということになりますから。
また、系を考え、外部から系に力が働かない限り、運動量はかならず保存されます。
それは内力でありさえすれば、摩擦等が作用する場合でも成り立ちます。
次の図のように物体が正面衝突する場合を考えてみます。
簡単のため、物体ABを共に質量 $m$ 、速度の大きさもともに $v$ とします。
まず、反発係数が $1$ のとき

$mv+m(-v)=m(-v)+mv=0$
そして反発係数が $0$ のとき

$mv+m(-v)=0+0=0$
図においてどのように衝突しようとも衝突の前後での運動量総和は常に $0$ です。
つまり、作用反作用の法則が成立していれば、いかなる場合も、系の運動量保存則が成り立つことがわかります。
もし作用反作用の法則がなりたっていない場合は、及ぼし合う力の大きさが違っているため、物体ABの加速度が変化し、そのため速度が変化して運動量保存則が成り立ちません。
また、力が作用するときにタイムラグがある場合も、同様に物体ABの加速度に違いが生じます。この場合も同様に、運動量保存則は成立しなくなります。
運動量保存則が成立するためには、作用反作用の法則が成り立つことが必要です。
平面での運動量保存則
速度はベクトル量です。よって、運動量 $mv$ も力積 $F\Delta t$ もベクトル量です。
ゆえに、ビリヤードの玉突きのような平面上の衝突についても運動量保存則は成り立っています。この場合は、x-y 方向に分解して考えるか、ベクトル図で考えてください。
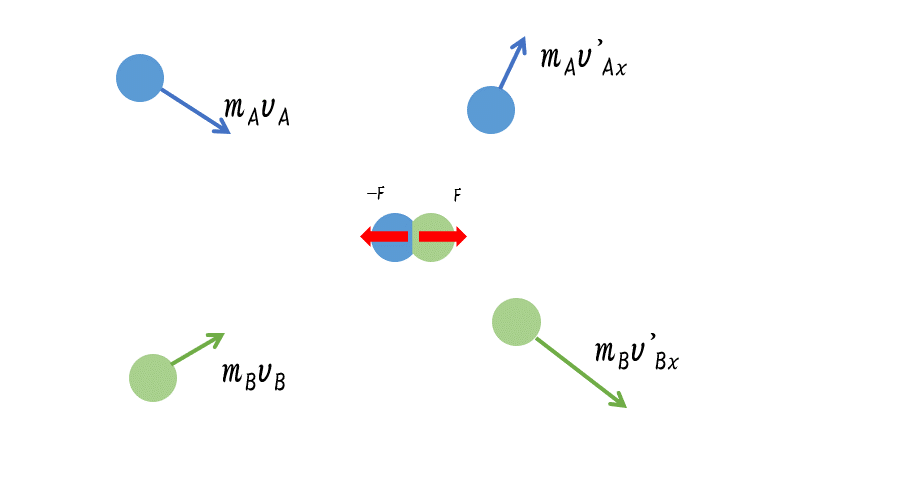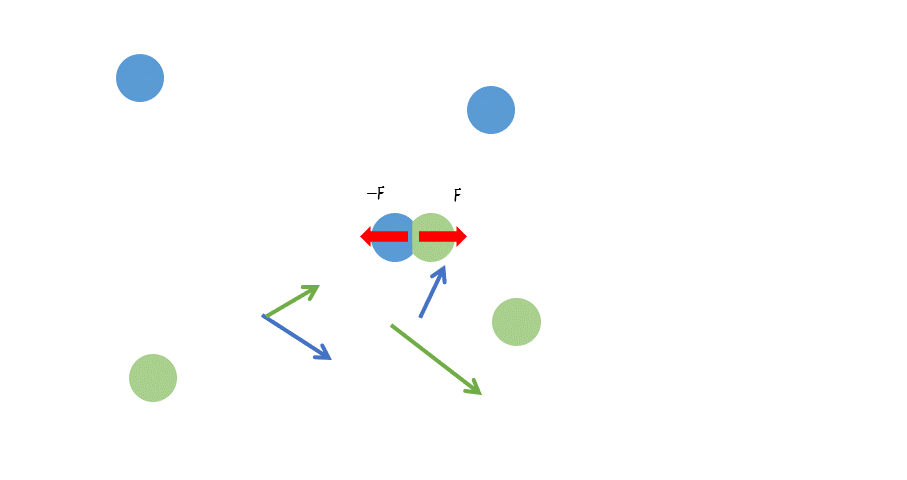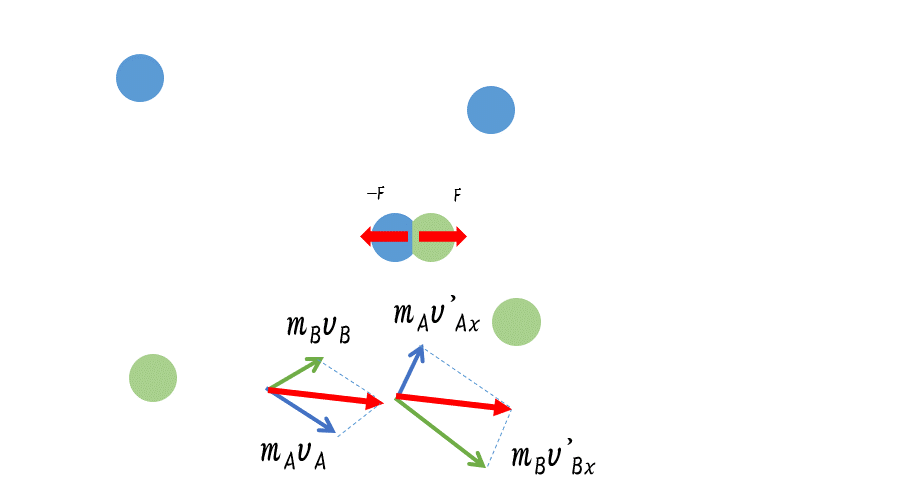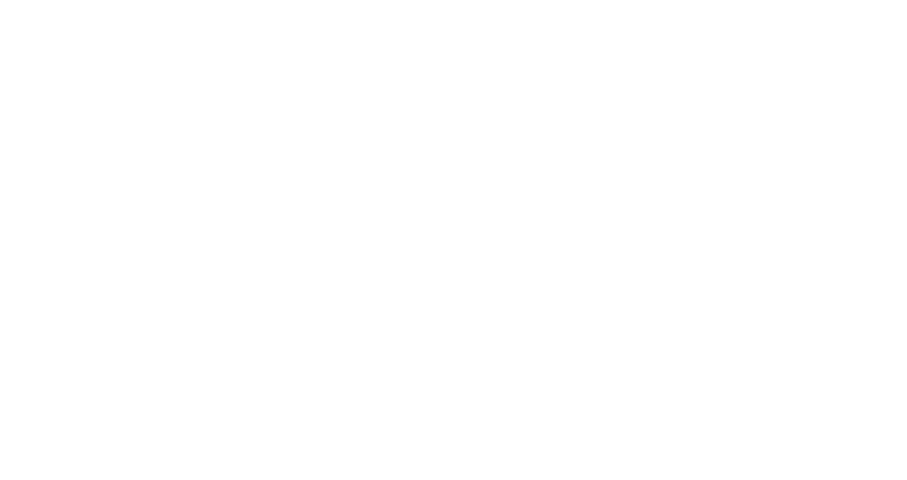
このとき、
$m_A\vec{v_A}+m_B\vec{v_B}=m_A\vec{v’_A}+m_B\vec{v’_B}$
が成り立ちます。
あるいは、図で運動量ベクトルを $x-y$ 方向に分解して、その成分で考えます。
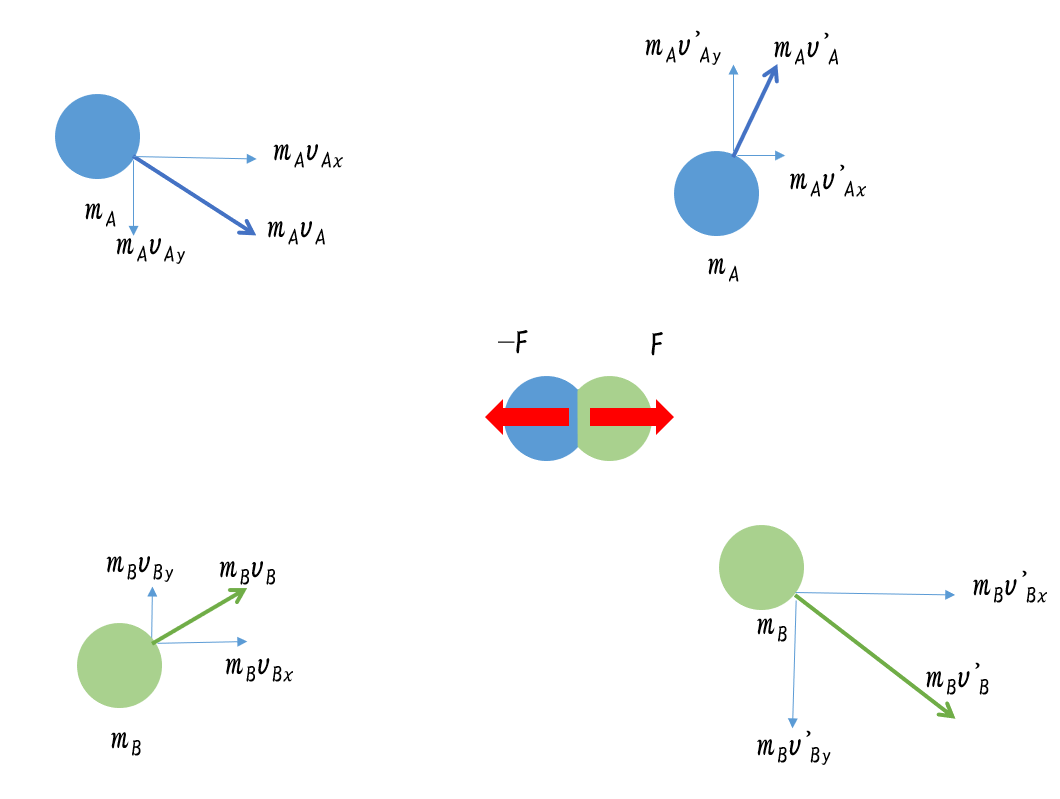
図より、
$m_Av_{Ax}+m_Bv_{Bx}=m_Av’_{Ax}+m_Bv’_{Bx}$
$m_Av_{Ay}+m_Bv_{By}=m_Av’_{Ay}+m_Bv’_{By}$
となります。
分裂時の運動量保存則
運動量保存則は、物体が爆発、分裂時にも成り立っています。
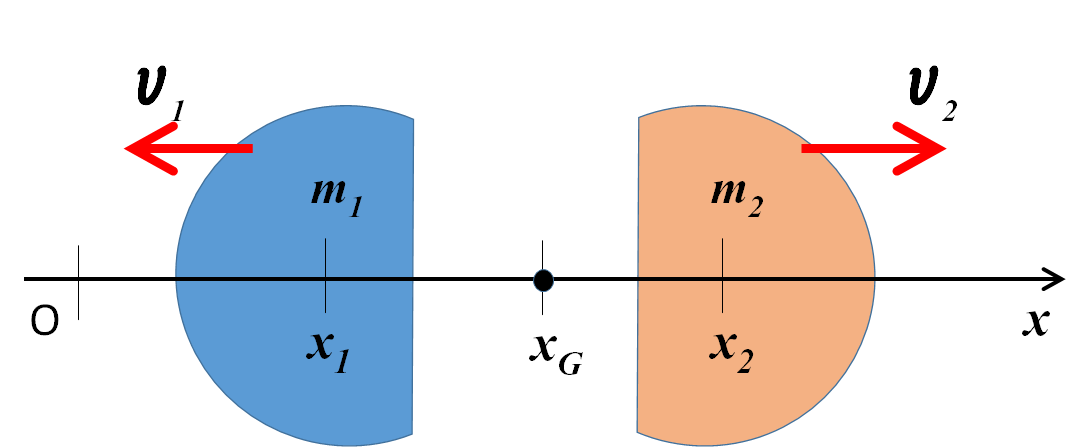
図は、静止していた物体が分裂する様子です。
質量 $M$ の物体が分裂して $m$ と$M-m$ の二つに分裂したとします。
その際に、物体Aは図の左方向に速さ $v_A$ で、Bは図の右に速さ $v_B$ で進んだとします。
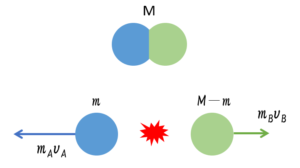
図の右向きを正として、運動量保存則を立ててみましょう。
まず最初は静止しているので運動量総和は $0$ です。
これがいつも保存されるため、分裂後の運動量の総和も $0$ となります。
$v_A$ は負の向きに進んでいます。
より、
$0=m(-v_{A})+(M-m)v_{B}$
となります。
もし、物体が分裂前に図の右方向に速さ $V$ で等速運動していた場合は、左辺の $0$ のかわりに、 $MV$ が入ります。
分裂する物体の重心位置の運動については
を参照してください。





































コメント