万有引力と位置エネルギー
第1宇宙速度と第2宇宙速度についてはこちらへ
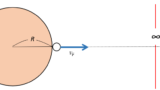
万有引力

万有引力 $f$ は、質量 $M$ の物体と、質量 $m$ の物体が距離 $r$ だけ離れているときに及ぼしあう力で、引力しかありません。その大きさは、万有引力定数を $G$ とすると、
$$f=G\dfrac{Mm}{r^2}$$
で示されます。
作用反作用の法則はこの場合も満たされており、それらの力は一直線上で等大・逆向きです。

よくある作用反作用の間違いあるあるですが、
机の上に置いた物体にかかる重力の反作用は?
という問いで、元気よく「垂直抗力!」と答えてはいけません。
この時の反作用は地球が受ける万有引力です。
作用反作用に関しては

重力と万有引力
これまでに学習した重力 $mg$ の原因というのは、地球と物体の間に働く万有引力です。
地球半径 $R$、地球質量 $M$ 、地球表面にある物体の質量 $m$ とすると、それらの間にはたらく万有引力の大きさ $f $ は、
$$f=G\dfrac{Mm}{R^2}$$
です。
地表では、$R$ 一定とみなし、地球表面近辺で万有引力は場所によらず一定として差し支えないでしょう。
そして、それが、質量 $m$ の物体にかかる、地表近辺での重力 $mg$ にほかなりませんから、
$$f=G\dfrac{Mm}{R^2}=mg$$
です。
したがって、 $GM=gR^2$ です。
これは、非常によく使う換算式ですのでここでしっかりと理解しておきましょう。
万有引力の位置エネルギー
重力 $mg$ に位置エネルギー $mgh$ を考えるように、万有引力による位置エネルギーを考えることができます。
位置エネルギーはその基準位置を示す必要がありますが、基準位置は原則、任意の位置にとることができます。
そのため、位置エネルギーは負になることもあり、それはそれでかまわないのです。
さて、万有引力による位置エネルギーを考えるときその基準位置は、一般には無限遠 $\infty$ をとります。
こうすると、無限遠での位置エネルギーが必ず $0$ になり、計算がラクです。

万有引力の場合も、その位置エネルギーの基準位置は変えてもかまわないのですが、地球中心は万有引力が無限大になってしまい、都合が悪いので取りません。
基準点をずらした場合の考え方は、次の記事で解説していますのでご覧ください。
重力 $mg$ による位置エネルギー
まず、重力 $mg$ による位置エネルギーについて考えてみましょう。
保存力による位置のエネルギーは、外力のする仕事で示すことができます。
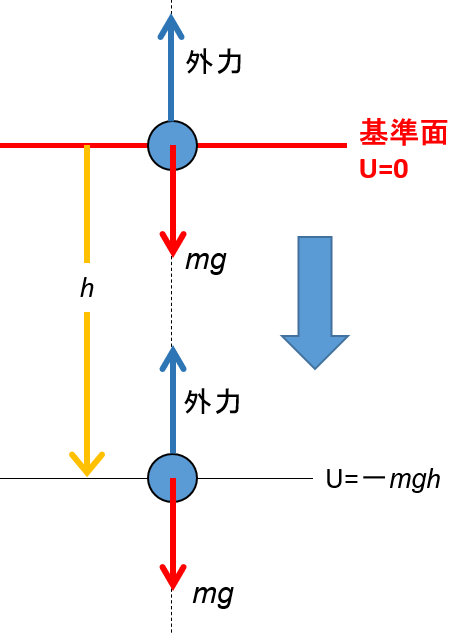
図のようにある外力で質量 $m$ の物体を静かに、図の基準点から $h$ の高さまで運ぶことを考えます。
このとき、外力の大きさは $mg$ としてかまいません。(つり合っているとして良い)
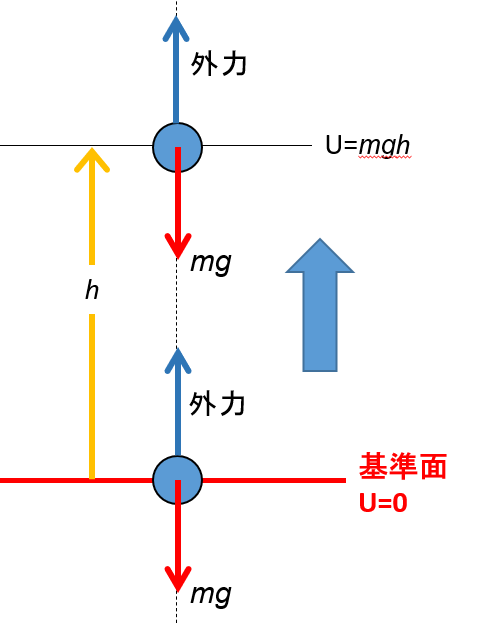
その時の仕事 $W$ は、$W=Fx$ より、
$$W=Fx=(mg)\times h=mgh$$
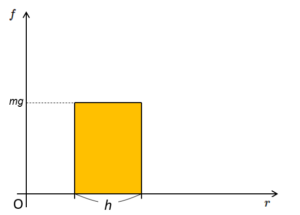
です。これは、図の $f-r $ グラフにおいて、四角形の面積を計算することと同じです。
このとき、この仕事 $W$ が、基準点より $h$ 高いところにある物体のもつ位置エネルギー $U$ です。
したがって、
$$U=mgh$$
です。
あるいはこのとき、運ぶ位置が、基準点より下にある場合は、
$$U=-mgh$$
となり、位置エネルギーは負になります。(図)
万有引力による位置エネルギー
では、万有引力の場合を考えます。
この場合の位置エネルギー基準は、無限遠 $\infty$ です。
(つまり、無限遠で 位置エネルギー = 0 です)
したがって、無限遠を基準点にとった位置エネルギーの値は、最大が $0$ で、普通は負の値になります。
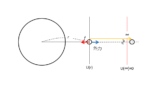
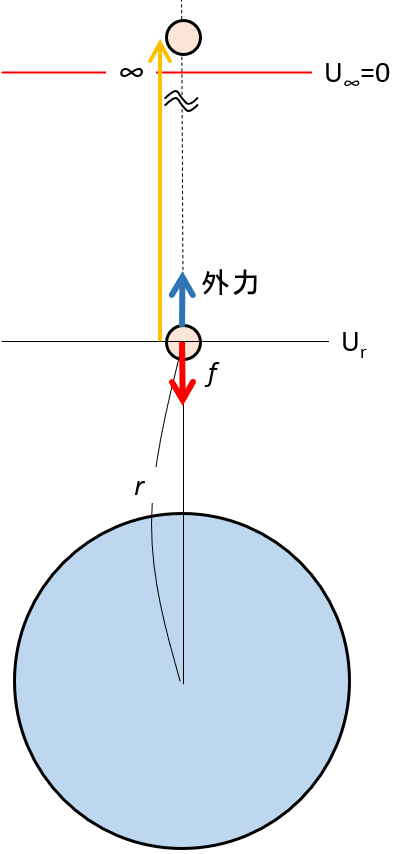
今、地球の中心から $r$ の距離のところにある質量 $m$ の物体が持つ位置エネルギーを考えます。
これは、この $r$ の位置から無限遠 $\infty$ まで万有引力に逆らいながら、ゆっくりと運ぶための仕事で計算できます。
この時必要な外力 $f’$ は万有引力と同じ大きさです。(つり合っていると考えられるため)
よって、$f’=G\dfrac{mM}{r^2}$ です。
しかし、このときの仕事 $W$ は、万有引力の大きさが $r$ によって違ってくるため、単純に $W=Fx$ の仕事の式を使うというわけにはいきません。
ではどうするか?
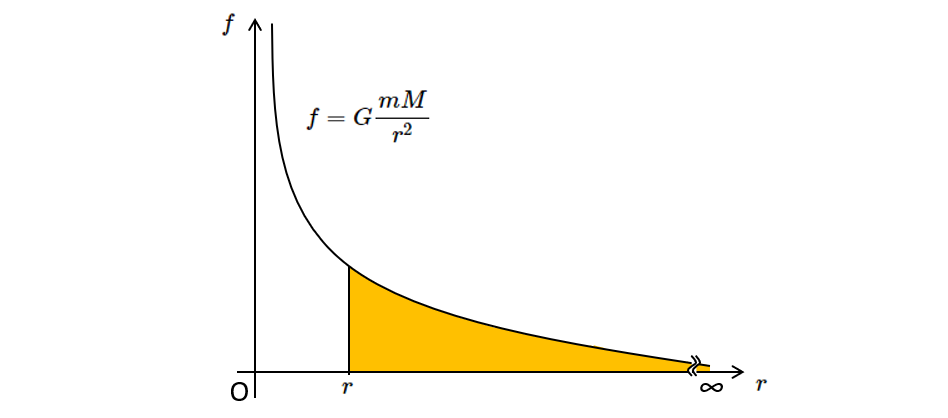
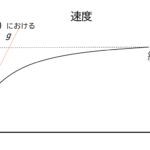
これは、$f-r$ グラフを描いてみましょう。
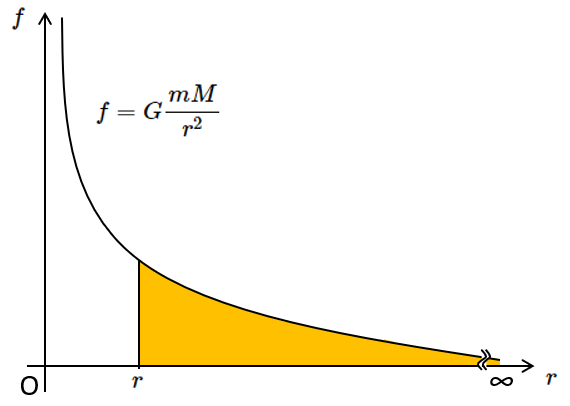
このとき、$r$ から $\infty$ までの $x$ 軸とグラフが囲む面積が仕事 $W$ の大きさと考えられます。
この面積を求めるには、$\int$ して求めます。
\begin{eqnarray}
W&=&\int^{\infty}_r G\dfrac{mM}{r^2}dr\\\\
&=&\left[ -G\dfrac{mM}{r} \right]^{\infty}_r\\\\
W&=&G\dfrac{mM}{r}
\end{eqnarray}
です。
$r$ の位置から基準点まで運ぶための仕事の大きさが $W=G\dfrac{mM}{r}$ ですから、$r$ の位置では、エネルギーとしては $G\dfrac{mM}{r}$ だけ低いところにあります。
したがって、$r$ の位置での万有引力による位置エネルギー $U$ は
$$U=-G\dfrac{mM}{r}$$
と示されます。




































コメント