「落体の跳ね返りによる総運動時間を求める」という問題がありますが、$v-t$ グラフを使うことで簡単に解くこともできます。
ここではその方法や、$v-t$ グラフ一般について解説しています。
最初のほうはよく知っているという人は、飛ばしてもかまいません。
簡単テクニックについては、この個所をお読みください。
v-t グラフの活用
今回お話ししたいことは、$v-t$ グラフについてです。
$v-t$ グラフについては、あまり重視していない方が多く、もったいない気がします。
$v-t$ グラフを用いれば、例えば「公式」なるものをド忘れした場合に、おおいに役立ちます。
なにより、$v-t$ グラフを用いれば複雑な計算から解放され、あっという間に問題が解けてしまうことさえまれではありません。

$v-t$ グラフを利用してエッセンス問題を解いています。
$v-t$ グラフとは、文字通り横軸に時間 $t$ 、縦軸に速度 $v$ をとったものです。
物体が等速直線運動しているときは、その $v-t$ グラフは $t$ 軸に平行な直線になります。
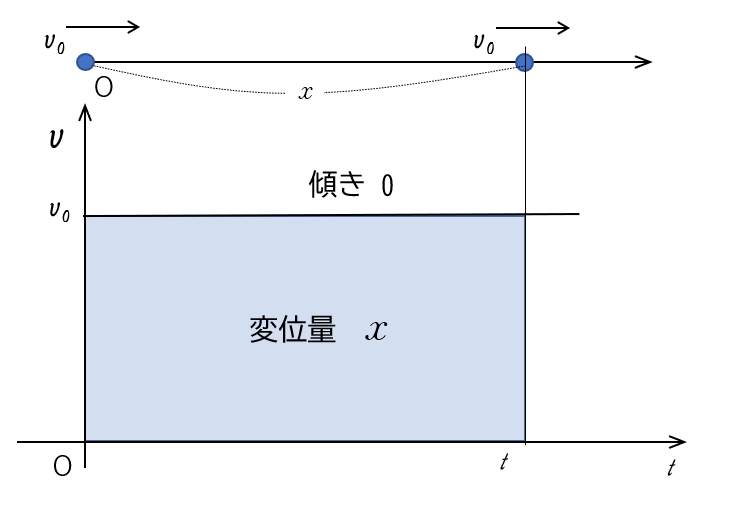
物体が等加速直線運動しているときは、ある傾きを持った直線になります。
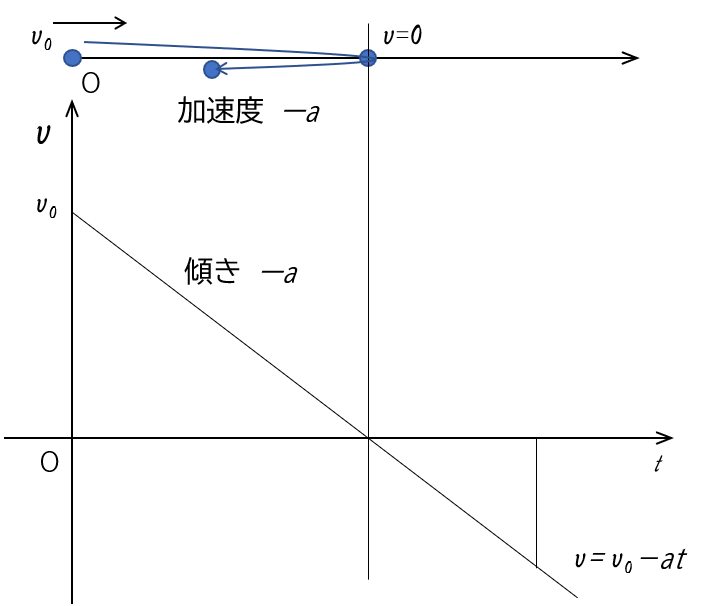
その直線の傾きが加速度を示しています。
そして、$t$ 軸との囲む面積が、その変位量 $x$ を示しています。
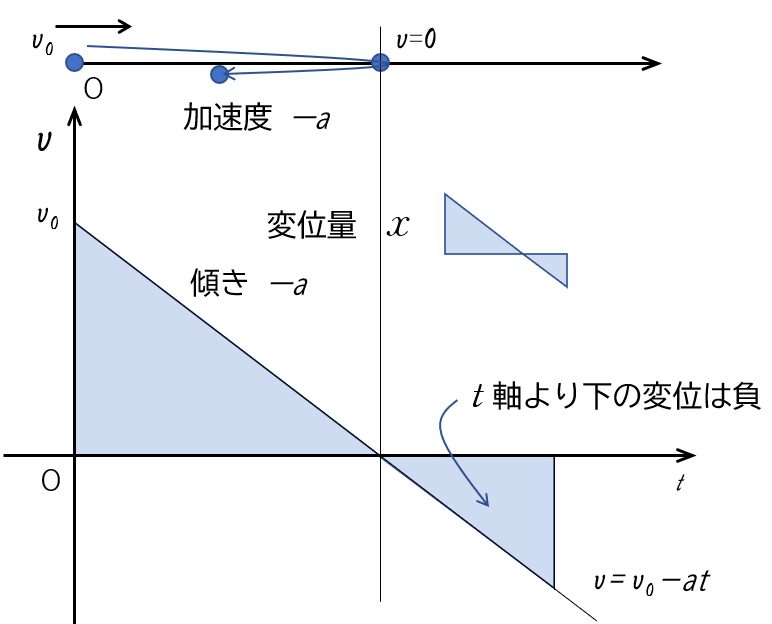
変位量(出発点からの位置)としては、 $t$ 軸より下の部分は負とします。
ただし、道のり(車の距離メーターの値)の場合は絶対値をとります。
落体の $v-t$ グラフ
ここでは、落体の運動についての基本的な知識を得ている、との前提でお話しします。

落体の運動についての基礎的なお話は以下のリンクからどうぞ!


落体の加速度
重力だけを受けて運動する物体の持つ加速度の大きさは、すべて $g$ です。
これは投げ上げの途中であろうと、投げおろし・自由落下・斜方投射であろうと関係なく、すべて鉛直下方に $g$ の加速度を持っています。
つまり、必ず鉛直下向きに $g$ なのです。
そしてこのことが、落体の $v-t$ グラフに特徴的な性質を持たせています。
すなわち、落体運動の $v-t$ グラフの傾きの大きさは必ず $g$ であり、すべての落体の $v-t$ グラフの傾きの大きさは同じで $g$ です。
では、まず自由落下から見ていきましょう。
自由落下
鉛直下向きを正の向きとしています。
自由落下ですから、初速度 $v_0=0$ です。
したがってその $v-t$ グラフは、
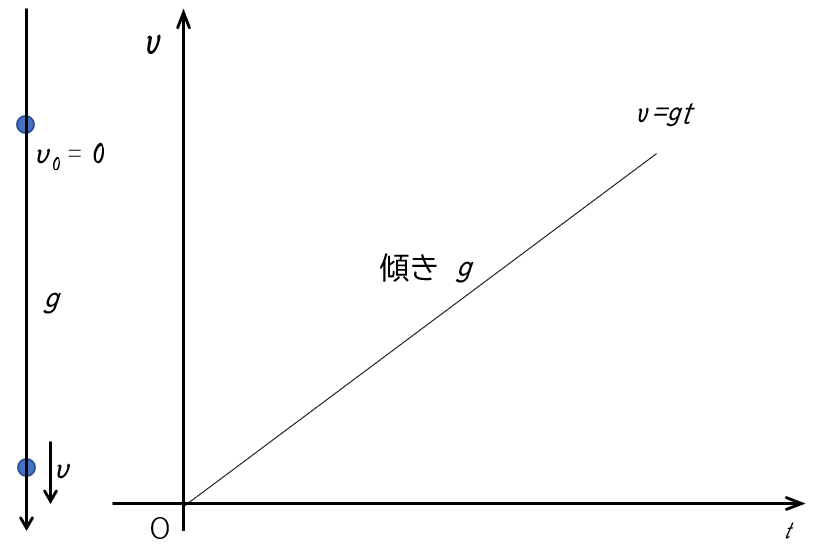
となり、グラフの傾きは $g$ です。
鉛直投げ上げ
鉛直上向きを正の向きとした場合、その $v-t$ グラフは、傾きが $-g$ です。
初速度 $v_0$ としています。
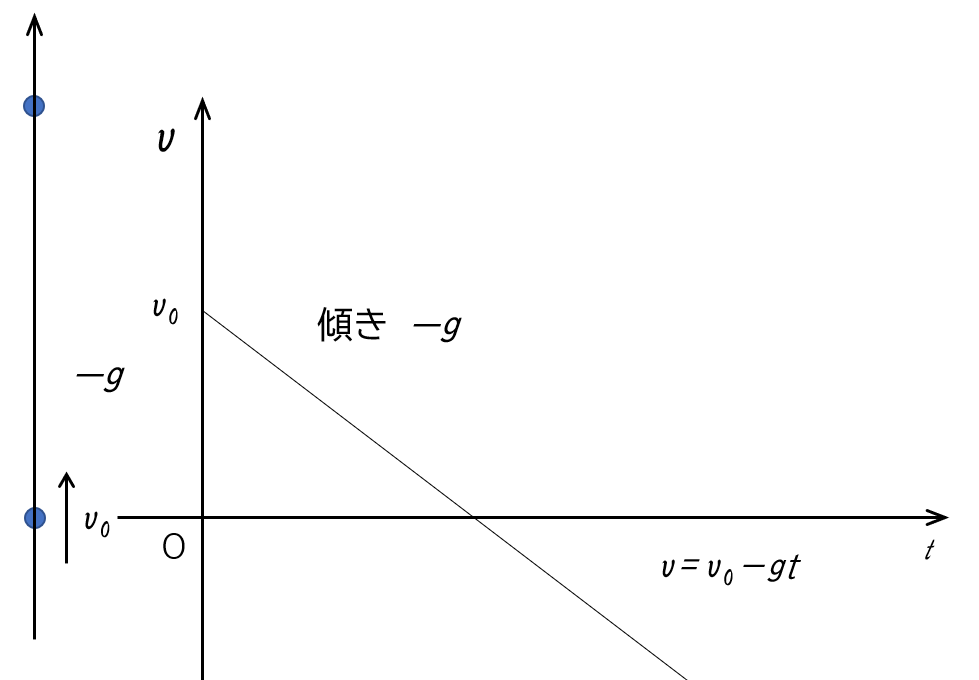
- 物体が最高点に達したときは $v=0$ です。
物体が最高点に達するまでにかかる時間 $t$ は、直線の傾きの大きさが $g$ であることから、簡単に $|g|=\dfrac{v_0}{t}$ として求めることができます。
すなわち、$t=\dfrac{v_0}{g}$ です。 - 最高点高さは、図の三角形の面積を求めることで得られます。
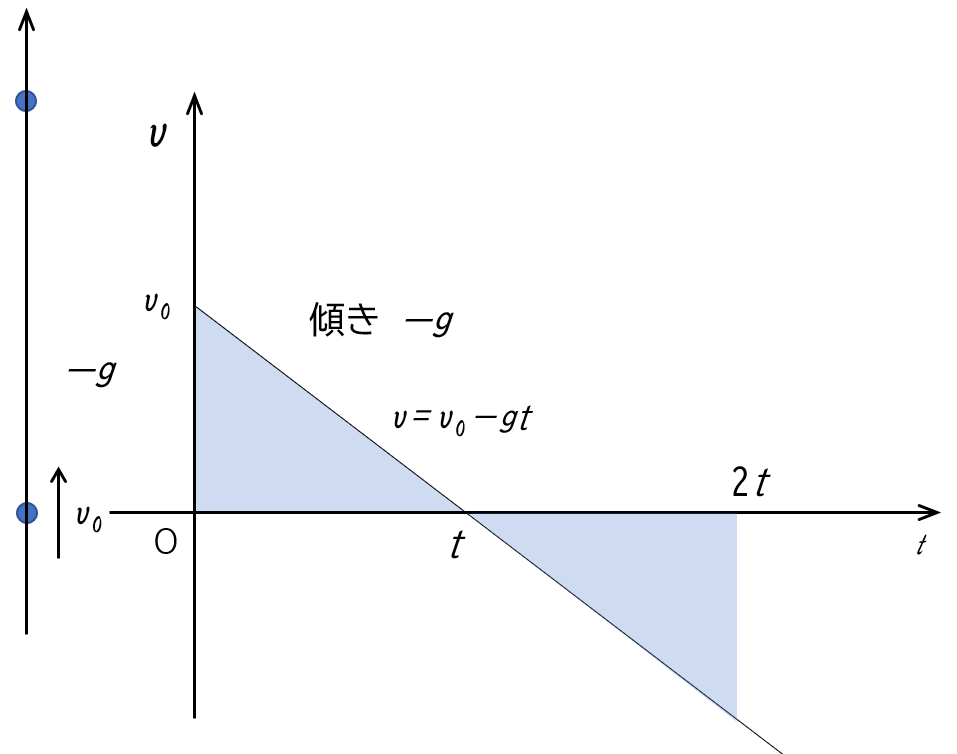
- 物体が出発点に戻るまでの時間は変位が $0$ になる時間ですから、図の二つの三角形が合同になる時です。
したがって、出発点に戻るまでの時間は $2t\:(=2\dfrac{v_0}{g})$ となることは自明です。
鉛直投げ下ろし
鉛直下向きを正の向きとした場合、その $v-t$ グラフの傾きは $g$ となります。
初速度 $v_0$ です。
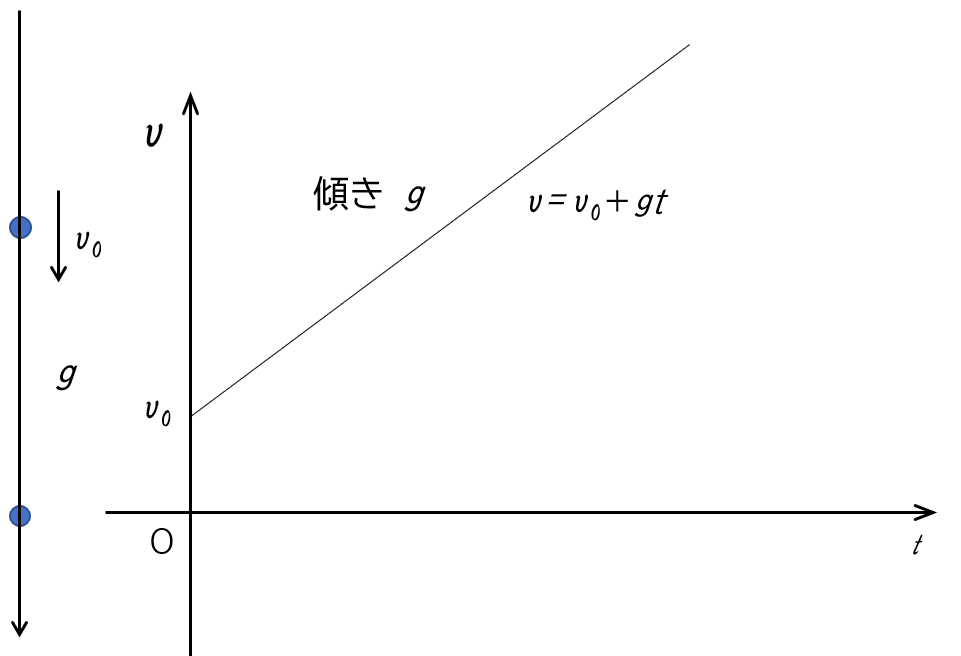
この時の $t$ 軸とグラフの囲む面積を求めることで、おなじみの「公式」 $x=v_0t+\dfrac{1}{2}gt^2$ を導出することができます。
地面で跳ね返る場合
地面で跳ね返る場合を考えましょう。
$v-t$ グラフを使うことでウソみたいに簡単になります。
高さ $h$ から初速度 $0$ で物体を落としたとします。
最初に物体を離してから地面に衝突するまでの時間を $t$ 、衝突する直前の速さを $v$ としましょう。
そして、物体と地面との反発係数を $e$ としておきます。$(0\leq e<1)$
そうすると速さ $v$ で最初に地面に衝突したのち、打ち上げられる速度は $-ev$ となります。

跳ね返り係数 $e$ の式は
$e=-\dfrac{v’}{v}$です。
よって、 $v’=-ev$ ですね。
$v$ 衝突前、$v’$ 衝突後の速度です
一度地面で跳ね返ったものが、再び地面に衝突するときの速度は $ev$ ですね。(エネルギー保存則)
したがって、地面で2度目に跳ね返って打ち上げられるときの速度は、 $-e^2v$ となります。
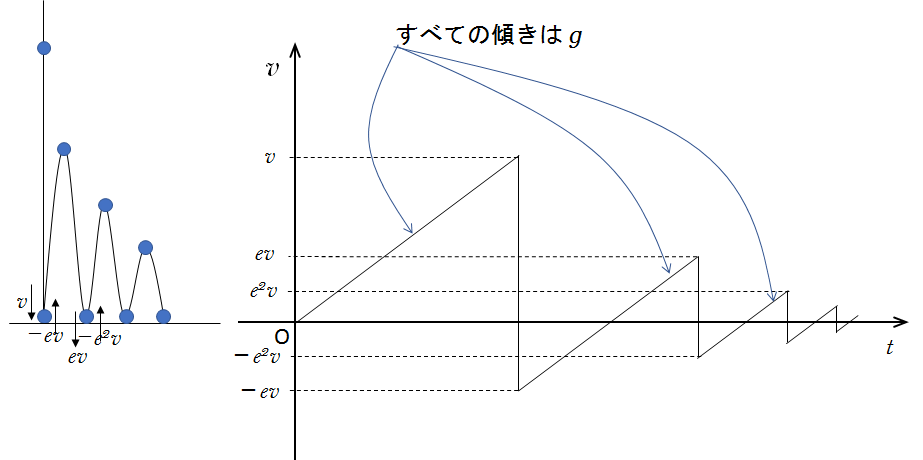
以降、これを繰り返して、最終的には速度 $0$ になります。
簡単テクニック
この運動は、重力による落体運動ゆえ、加速度はすべて $g$ です。
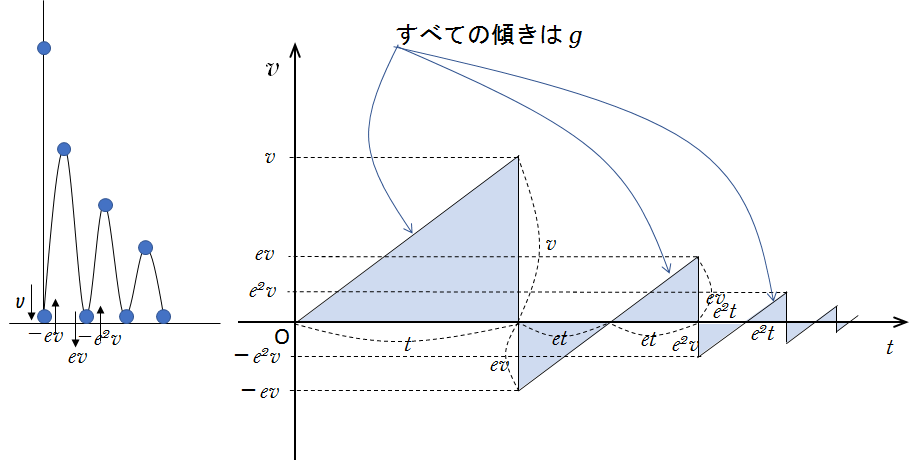
そのため、グラフの傾きはすべて同じで $g$ です。
したがって、図のグラフで $t$ 軸と囲まれる三角形はすべて相似形です。
速さは $ v\:\:\rightarrow\:\ ev\:\:\rightarrow\:\ e^2v\:\:\rightarrow\:\ e^3v\:\:\cdots$ となりますから、相似三角形の関係から、各三角形の底辺の長さも $t\:\:\rightarrow\:\ et\:\:\rightarrow\:\ e^2t\:\:\rightarrow\:\ e^3t\:\:\cdots$ のように変化していきます。
よって、この跳ね返りが収まるまでどれくらいの時間が必要か?という問題に対しては、その時間を $T$ とすると、
\begin{eqnarray}
T&=&t+2et+2e^2t+2e^3t+ \cdots+2e^nt+\cdots\\\\
&=&-t+2t(1+e+e^2+e^3+\cdots+e^n+\cdots)\\
\end{eqnarray}
を計算すればいいことになります。
ここで、$1+e+e^2+e^3+\cdots+e^n+\cdots \:\:\:\:\:\: (0\leq e <1)$ は、
\begin{eqnarray}
1+e+e^2+e^3+\cdots+e^n+\cdots&=&\sum^{\infty}_0(e^n)\\\\
&=&\dfrac{1}{1-e}
\end{eqnarray}
です。
$t$ は地面までの最初の落下時間、そして最初に物体があった高さは $h$ でした。
ここで、 $y=\dfrac{1}{2}gt^2$ から、$t$ は、
$$t=\sqrt{\dfrac{2h}{g}}$$
となります。
よってこれらより、
\begin{eqnarray}
T&=&-t+2t\left(\dfrac{1}{1-e} \right)\\\\
&=&t \left( -1+\dfrac{2}{1-e} \right) \\\\
&=&\sqrt{\dfrac{2h}{g}} \cdot \dfrac{1+e}{1-e}
\end{eqnarray}
が導かれました。




































コメント